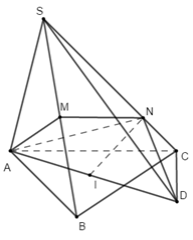
Cho hình chóp có SA vuông góc (ABC) \( \;\left( {AB{\rm{ }} = 3,{\rm{ }}AC = 2,\widehat {BAC} = {\rm{ }}{{60}^0}} \right)\). Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu ngoại tiếp chóp ABCNM.

Câu hỏi liên quan

• Hình chóp nào sau đây luôn nội tiếp được mặt cầu?

• Mặt cầu (S) có tâm \(I(1 ; 2 ;-1) \) và tiếp xúc với mặt phẳng \((P): x-2 y-2 z-8=0\) có phương trình là 

• Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1, 2, 4. Tổng độ dài đường kính của hai quả bóng đó.

ZUNIA12

• Cho hình lập phương ABCD.A’B’C’D’ cạnh a.  Tính diện tích mặt cầu đi qua tất cả các đỉnh  của hình lập phương.

• Nếu một khối cầu có bán kính bằng R thì có thể tích bằng

• Cho mặt cầu \(S\left( O;R \right),A\) là một điểm ở trên mặt cầu \(\left( S \right)\) và \(\left( P \right)\) là mặt phẳng đi qua A sao cho góc giữa OA và (P) bằng \({{60}^{0}}.\) Diện tích của đường tròn giao tuyến bằng:

• Phương trình mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;0; – 1} \right)\) và đi qua điểm \(A\left( {2;2; – 3} \right)\) là:

• Cho hình chóp đều \(S.ABC\) có đường cao \(SH=a\); góc \(SAB\) bằng 45 độ. Bán kính mặt cầu ngoại tiếp hình chóp \(S.ABC\) là

• Trong không gian Oxyz, tìm tất cả các giá trị của m để phương trình \({x^2} + {y^2} + {z^2} + 4x – 2y + 2z + m = 0\) là phương trình của một mặt cầu.

• Phương trình nào sau đây là phương trình mặt cầu có tâm \(I\left( { – 1;1;0} \right){\rm{ }}?\)

• Biết rằng đường thẳng d: \(\left\{ \begin{array}{l} x = 2 + 3t\\ y = t\\ z = - 1 - t \end{array} \right.\) là tiếp tuyến của mặt cầu tâm I(0;0;1). Bán kính R của mặt cầu đó là

• Khối cầu có thể tích \( \frac{{32\pi {a^3}}}{3}\) thì bán kính bằng:

• Trong không gian với hệ trục tọa độ Oxyz, mặt cầu \(\left( S \right):{\left( {x + 2} \right)^2} + {\left( {y – 1} \right)^2} + {z^2} = 4\) có tâm I và bán kính R lần lượt là

• Cho một mặt cầu có diện tích là S, thể tích khối cầu đó là V. Tính bán kính R của mặt cầu.

• Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt cầu tâm \(I\left( {1;\,2;\, – 4} \right)\) và thể tích của khối cầu tương ứng bằng \(36\pi \)?

• Mặt cầu đi qua các đỉnh của một hình đa diện thì nó được gọi là:

• Một mặt cầu có diện tích \(16\pi \). Tính bán kính mặt cầu đó.

• Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = 2a, AC = a. Mặt bên SAB, SCA lần lượt là các tam giác vuông tại B và C. Biết rằng thể tích khối chóp S.ABC bằng \(\frac{2}{3}{a^3}\). Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:

• Cho bát diện đều, tính tỷ số giữa thể tích khối cầu nội tiếp và thể tích khối cầu ngoại tiếp hình bát diện đều đó.

• Trong không gian Oxyz, cho mặt cầu \((S):{x^2} + {y^2} + {z^2} – 2x + 4y – 4z – m = 0\) có bán kính R = 5. Giá trị của tham số m bằng