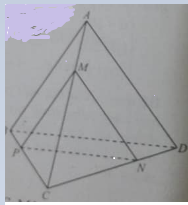
Cho hình chóp (S.ABCD )có đáy ABCD là hình thang (AB//CD). Gọi I,J lần lượt là trung điểm của các cạnh AD, BC và G là trọng tâm tam giác (SAB ). Biết thiết diện của hình chóp cắt bởi mặt phẳng (IJG) là hình bình hành. Hỏi khẳng định nào sao đây đúng?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiVì (IJG)∩(SAB)={G} ta có IJ//AB vì IJ là đường trung bình của hình thang ABCD
(IJG)∩(SAB)=Gx//AB//IJ.Gọi E=Gx∩SA,F=Gx∩SB
(IJG)∩(SAD)=EI;(IJG)∩(ABCD)=IJ;(IJG)∩(SBC)=JF
Suy ra thiết diện (IJG) và hình chóp là hình bình hành IJFE⇔IJ=EF(1)
vì G là trọng tâm tam giác \( SAB \Leftrightarrow SG = \frac{2}{3}GH \Rightarrow EF = \frac{2}{3}AB{\mkern 1mu} {\mkern 1mu} \left( 2 \right)\)
và \( IJ = \frac{{AB + CD}}{2}{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 3 \right)\) vì JI là đường trung bình của hình thang ABCD
Từ (1),(2) và (3) \( \Rightarrow \frac{2}{3}AB = \frac{{AB + CD}}{2} \Leftrightarrow 4AB = 3AB + 3CD \Leftrightarrow AB = 3CD\)
Đáp án cần chọn là: C
.PNG)