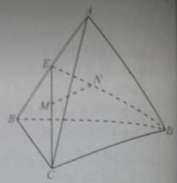
Cho hình chóp (S.ABCD ) có đáy (ABCD ) là hình bình hành. Gọi M là trung điểm SD, N là trọng tâm tam giác SAB. Đường thẳng MN cắt mặt phẳng (SBC) tại điểm I. Tính tỷ số \( \frac{{IN}}{{IM}}\)
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiGọi J;E lần lượt là trung điểm SA;AB.
Trong mặt phẳng (BCMJ) gọi I=MN∩BC
Ta có: IM là đường trung tuyến của tam giác SID.
Trong tam giác ICD ta có BE song song và bằng \(
\frac{1}{2}CD\) nên suy ra BE là đường trung bình của tam giác ICD⇒E là trung điểm ID⇒SE là đường trung tuyến của tam giác SID.
Ta có: N=IM∩SE⇒N là trọng tâm tam giác \( SID \Rightarrow \frac{{IN}}{{IM}} = \frac{2}{3}\)
Đáp án cần chọn là: D
ADMICRO
YOMEDIA
ZUNIA9
.PNG)