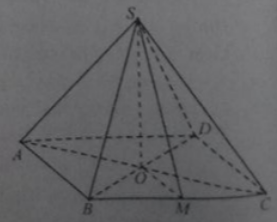
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và S, SA vuông góc với mặt phẳng đáy. Tính cô-sin góc giữa 2 đường thẳng SD và BC biết \(AD=D C=a, A B=2 a, S A=\frac{2 \sqrt{3} a}{3}\)

Câu hỏi liên quan

• Cho hình lăng trụ tam giác đều \(A B C . A^{\prime} B^{\prime} C^{\prime} \text { có } A B=a\,và\,A A^{\prime}=\sqrt{2} a\). Góc giữa hai đường thẳng AB' và BC' bằng

• Cho hình chóp S.ABC có tất cả các cạnh đều bằng a. Gọi I, J lần lượt là trung điểm của SA, BC. Tính số đo của góc hợp bởi IJ và SB.

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. \(SA \bot \left( {ABCD} \right)\), SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60^o.

ZUNIA12

• Trong các mệnh đề sau, mệnh đề nào đúng?

• Lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a. Gọi M là điểm trên cạnh AA' sao cho \(AM = \frac{{3a}}{4}\). Tang của góc hợp bởi hai mặt phẳng (MBC) và (ABC) là:

• Cho hình chóp S ABCD . có đáy ABCD là hình vuông tâm O . Biết \(S O \perp(A B C D)\), \(S O=a \sqrt{3}\) và đường tròn ngoại tiếp ABCD có bán kính bằng a . Gọi \(\alpha\) là góc hợp bởi mặt bên (SCD) với đáy. Khi đó \(\tan \alpha=?\)

• Cho hình chóp S.ABC có \(S A \perp(A B C)\) và đáy ABC vuông ở A . Khẳng định nào sau đây sai ? 

• Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của hình chóp S.ABCD là \(\frac{{{a}^{3}}\sqrt{15}}{6}\). Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là:

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết \(SO \bot \left( {ABCD} \right)\), \(SO = a\sqrt 3 \) và đường tròn ngoại tiếp ABCD có bán kính bằng a. Gọi \(\alpha\) là góc hợp bởi mặt bên (SCD) với đáy. Khi đó \(\tan \alpha = ?\)

• Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc \(\widehat {BAD} = {60^0}\). Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và \(SO = \frac{{3a}}{4}\). Gọi E là trung điểm BC và F là trung điểm BE. Góc giữa hai mặt phẳng (SOF) và (SBC) là

• Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC = 2a. Các cạnh bên vuông góc với đáy và AA' = a. Khẳng định nào sau đây sai ?

• Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc giữa cạnh bên với mặt phẳng đáy bằng ∝

  

  Tan của góc giữa mặt bên và mặt đáy bằng:

• Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

• Cho hai đường thẳng chéo nhau a và b đồng thời \(a \bot b\). Chỉ ra mệnh đề đúng trong các mệnh đề sau:

• Cho hình lăng trụ đứng ABC.A'B'C' có AB = AA' = a, BC = 2a, \(CA = a\sqrt 5 \). Khẳng định nào sau đây sai?

• Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân ở A. H là trung điểm BC. Khẳng định nào sau đây sai ?

• Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến \(\Delta\). Lấy A, B cùng thuộc \(\Delta\) và lấy C trên (P), D trên (Q) sao cho \(AC \bot AB,BD \bot AB\) và AB = AC = BD. Thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng \((\alpha)\) đi qua A và vuông góc với CD là hình gì?

• Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, với AB = c, AC = b, cạnh bên AA' = h. Mặt phẳng (P) đi qua A' và vuông góc với B'C.Thiết diện của lăng trụ cắt bởi mặt phẳng (P) có hình:

  

• Cho hình lăng trụ ABCD.A'B'C'D'. Hình chiếu vuông góc của A' lên (ABC) trùng với trực tâm H của tam giác ABC. Khẳng định nào sau đây không đúng?

• Cho tứ diện đều ABCD cạnh a= 12, gọi (P) là mặt phẳng qua B và vuông góc với AD. Thiết diện của (P) và hình chóp có diện tích bằng