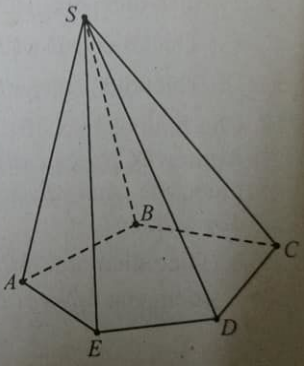
Cho hình chóp S.ABCD có đáy là hình thang với các cạnh đáy là AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm của tamg iacs SAB. Tìm điều kiện của AB và CD để thiết diện của (GIJ) với hình chóp S.ABCD là hình bình hành.

Câu hỏi liên quan

• Cho tứ giác ABCD và các điểm M, N phân biệt thuộc cạnh AB, các điểm P, Q phân biệt thuộc cạnh CD. Phát biểu nào sau đây là đúng?

• Nếu hai mặt phẳng  phân biệt có điểm chung thì tất cả những điểm chung của chúng sẽ nằm trên:

• Với giả thiết: tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA, AC và BD. Hãy cho biết trong các mệnh đề sau, mệnh đề nào đúng?

ZUNIA12

• Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?

• Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I,J lần lượt là trung điểm của AB và BC. Khi đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng song song với:

• Cho hình tứ diện ABCD. Khẳng định nào sau đây là đúng?

• Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (MBC) và mp (NDA) là:

• Thiết diện của mặt phẳng với tứ diện

• Cho hình chóp S.ABCD có đáy là hình thang ABCD( AD / /BC) . Gọi I là giao điểm của AB và DC , M là trung điểm SC . DM cắt mặt phẳng (SAB) tại J . Khẳng định nào sau đây sai?

• Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi I , J lần lượt là trung điểm SA và SB . Khẳng định nào sau đây là sai?

• Cho tứ diện ABCD và 3 điểm E, F, G lần lượt nằm trên 3 cạnh AB, BC, CD mà không trùng với các đỉnh, thiết diện của hình tứ diện ABCD khi cắt bởi mp(EFG) là:

• Cho hình chóp S.ABCD . Gọi I là trung điểm của SD , J là điểm trên SC và không trùng  điểm SC . Giao tuyến của hai mặt phẳng (ABCD) và (AIJ) là:

• Cho hình chóp S.ABCD có đáy là hình bình hành. M là trung điểm của SC. Tìm thiết diện của (MAB) với hình chóp.

• Cho hai đường thẳng a và b chéo nhau. Những phát biểu nào sau đây là sai?

  (1) tồn tại hai đường thẳng c, d song song với nhau, mỗi đường đều cắt cả a và b.

  (2) không thể tồn tại hai đường thẳng c, d phân biệt, mỗi đường đều cắt cả a và b.

  (3) không thể tồn tại một đường thẳng cắt cả a và b.

• Có một và chỉ một mặt phẳng đi qua

• Phát biểu nào sau đây là đúng?

  

• Tìm phát biểu sai ?

• Cho hình chóp S.ABCD có đáy là hình thang ABCD (AD//BC). Gọi M là trung điểm CD . Giao tuyến của hai mặt phẳng(MSB) và (SAC) là:

• Một mặt phẳng hoàn toàn được xác định nếu biết điều nào sau đây?

• Cho 4 điểm không đồng phẳng A, B, C, D. Khi đó giao tuyến của mp (ABC) và mp (BCD) là: