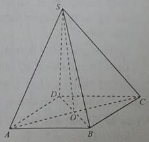
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2 và cạnh bên bằng \(2\sqrt 2 \). Khi đó góc giữa cạnh bên và đáy bằng

Câu hỏi liên quan

• Cho lăng trụ đều ABC.A’B’C’ có cạnh đáy bằng 2a, cạnh bên bằng a. Gọi M là trung điểm của BC. Tính góc giữa đường thẳng A’M và mặt phẳng đáy

• Mệnh đề nào sau đây có thể sai?

•  Cho hình chóp S.ABCD , đáy ABCD là hình vuông cạnh bằng a và \(S A \perp(A B C D)\). Biết \(S A=\frac{a \sqrt{6}}{3}\) . Tính góc giữa SC và (ABCD)?

ZUNIA12

• Cho lăng trụ đứng ABC.A’B’C’, có đáy là tam giác đều cạnh a, cạnh bên AA’ = a. Gọi N là trung điểm của CC’ và \(\varphi \) là góc giữa đường thẳng AP và mặt phẳng \(\left( {A’BC} \right)\). Khẳng định nào sau đây đúng?

• Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh \(SA \bot \left( {ABC} \right)\) và SA = 2a, gọi M là trung điểm của SC. Tính cos của góc \(\alpha \) là góc giữa đường thẳng BM và \(\left( {ABC} \right)\).

• Cho hình chóp S.ABC, có cạnh bên \(SA \bot \left( {ABC} \right)\). Góc giữa đường thẳng SB và đáy là góc nào dưới đây?

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông, hình chiếu của S lên mặt phẳng \(\left( {ABCD} \right)\) là điểm H sao cho \(2\overrightarrow {HA} + \overrightarrow {HB} = \overrightarrow 0 \). Góc giữa đường thẳng SB và đáy bằng \({45^0}\). Tính cos góc giữa đường thẳng SD và mặt phẳng \(\left( {SBC} \right)\).

• Cho hình chóp S ABC . có \(S A \perp(A B C)\) và tam giác ABC vuông ở B . AH là đường cao của tam giác SAB . Khẳng định nào sau đây sai ?

• Cho lăng trụ đứng ABC.A’B’C’, có đáy là tam giác đều cạnh a, cạnh bên AA’ = 2a. Gọi N là trung điểm của BB’ và \(\varphi \) là góc giữa đường thẳng AN và mặt phẳng \(\left( {A’BC} \right)\). Khẳng định nào sau đây đúng?

• Cho hình chóp S.ABCD đáy là hình thoi tâm O và SA = SC, SB= SD. Đường thẳng BC vuông góc với đường thẳng

• Cho tứ diện S.ABC có đáy ABC là tam giác vuông cân tại B, các tam giác SAB và SBC lần lượt là các tam giác vuông tại A và C. Góc giữa đường thẳng SA và mặt phẳng \(\left( {ABC} \right)\) bằng \(45^\circ \). Gọi H là hình chiếu vuông góc của S lên \(\left( {ABC} \right)\) và M là trung điểm của đoạn SA. Tính góc giữa đường thẳng HM mặt phẳng \(\left( {SBC} \right)\).

• Cho hình chóp S.ABCD  có đáy ABCD là hình thoi, O là giao điểm của 2 đường chéo và SA= SC . Các khẳng định sau, khẳng định nào đúng? 

• Cho hình tứ diện OABC có OA, OB, OC đôi một vuông góc. Nếu I là hình chiếu của điểm O trên mặt phẳng (ABC) thì I là:

• Cho tứ diện ABCD có \(A B=A C \text { và } D B=D C\) . Khẳng định nào sau đây đúng? 

• Cho hình lập phương ABCD.A’B’C’D’. Gọi M là trung điểm của cạnh BC. Tính \(cosin\) góc giữa đường thẳng AM và mặt phẳng \(\left( {A’CD} \right)\)

• Cho hình chóp đều, chọn mệnh đề sai trong các mệnh đề sau:

• Cho lăng trụ đều ABC.A’B’C’ có tất cả các cạnh đều bằng nhau và bằng a. Tính \(\cos in\) góc giữa đường thẳng AC’ và mặt phẳng \(\left( {A’BC} \right)\)

• Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M,N lần lượt là trung điểm của BC và SD. Gọi \(\alpha \) là góc giữa đường thẳng MN và đáy. Khẳng định nào sau đây đúng?

• Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt 6 \). Gọi M là trung điểm của SC. Tính góc giữa đường thẳng BM và \(\left( {ABCD} \right)\)

• Cho hai đường thẳng phân biệt a,b và mặt phẳng (P), trong đó \(a \perp(P)\). Mệnh đề nào sau đây là sai?