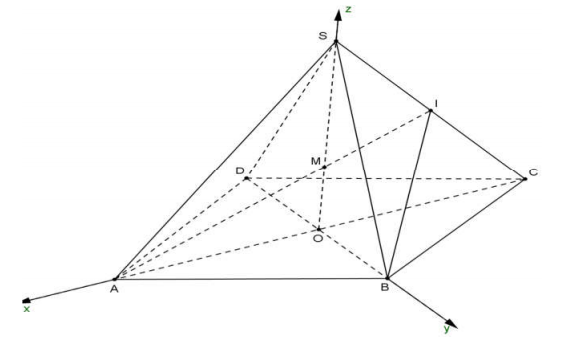
Cho hình chóp tứ giác đều S ABCD . có cạnh đáy bằng a và chiều cao bằng h. Gọi I là trung điểm cạnh bên SC . Tính khoảng cách từ S đến mặt phẳng
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi O là giao điểm của AC và BD . Ta có \(O A=O B=O C=\frac{a \sqrt{2}}{2}\).
Chọn hệ trục tọa độ Oxyz có gốc tọa độ O , tia Ox chứa A , tia Oy chứa B , tia Oz chứa S .
Khi đó \(A\left(\frac{a \sqrt{2}}{2} ; 0 ; 0\right), B\left(0 ; \frac{a \sqrt{2}}{2} ; 0\right), C\left(\frac{-a \sqrt{2}}{2} ; 0 ; 0\right), S(0 ; 0 ; h)\)
Gọi M là giao điểm của SO và AI .
Tam giác SAC có M là giao điểm của hai đường trung tuyến nên M là trọng tâm, do đó \(M\left(0 ; 0 ; \frac{h}{3}\right)\).
Mặt phẳng (AIB) đi qua A, B, M nên có phương trình \(:\frac{x}{\frac{a \sqrt{2}}{2}}+\frac{y}{\frac{a \sqrt{2}}{2}}+\frac{z}{\frac{h}{3}}=1\)
\(\Leftrightarrow \frac{\sqrt{2}}{a} x+\frac{\sqrt{2}}{a} y+\frac{3}{h} z-1=0\)
Do đó khoảng cách từ S đến mặt phẳng (AIB) là \(d=\frac{\left|\frac{3}{h} \cdot h-1\right|}{\sqrt{\frac{2}{a^{2}}+\frac{2}{a^{2}}+\frac{9}{h^{2}}}}=\frac{2 a h}{\sqrt{4 h^{2}+9 a^{2}}}\)