Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AD = 2 và \(AA’ = 2\sqrt 2 \) (tham khảo hình vẽ bên dưới).
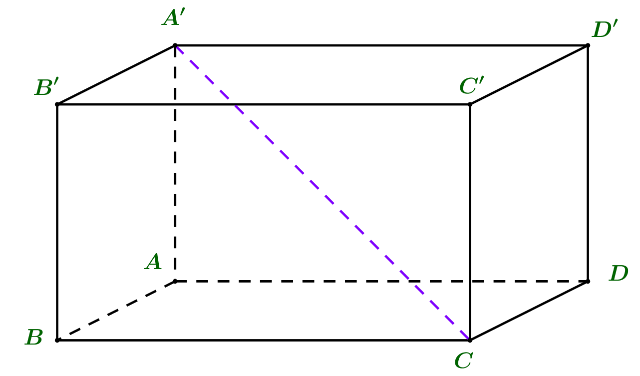
Góc giữa đường thẳng CA’ và mặt phẳng \(\left( {ABCD} \right)\) bằng
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Môn: Toán Lớp 11
Lời giải:
Báo sai.png)
Hình chiếu vuông góc của A’C lên đáy \(\left( {ABCD} \right)\) là AC, cho nên:
\(\left( {AC’,\left( {ABCD} \right)} \right) = \left( {AC’,AC} \right) = \widehat {ACA’}\)
Áp dụng định lý Pytago cho tam giác vuông ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} = {2^2} + {2^2} = 8 \Rightarrow AC = 2\sqrt 2 \).
Trong tam giác vuông ACA’ có: \(\tan \widehat {ACA’} = \frac{{AA’}}{{AC}} = \frac{{2\sqrt 2 }}{{2\sqrt 2 }} = 1 \Rightarrow \widehat {ACA’} = 45^\circ \).
Vậy góc giữa đường thẳng AC và đáy là \(45^\circ \).
ADMICRO
YOMEDIA
ZUNIA9
.png)