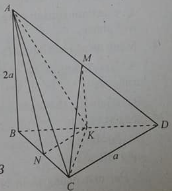
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là điểm thỏa mãn \(\overrightarrow {DM} = 3\overrightarrow {MC} \). Gọi \(\varphi \) là góc giữa đường thẳng SM và mặt phẳng \(\left( {SBC} \right)\). Khẳng định nào sau đây đúng?

A. \(\sin \varphi = \frac{{\sqrt {87} }}{{58}}\)

B. \(\sin \varphi = \frac{{\sqrt {15} }}{{40}}\)

C. \(\sin \varphi = \frac{{\sqrt 3 }}{3}\)

D. \(\sin \varphi = \frac{{\sqrt {87} }}{{116}}\)

Suy nghĩ và trả lời câu hỏi trước khi xem đáp án

Môn: Toán Lớp 11

Chủ đề: Quan hệ vuông góc trong không gian

Bài: Đường thẳng vuông góc với mặt phẳng

Lời giải:

Báo sai

Kẻ \(SO \bot AB \Rightarrow SO \bot \left( {ABCD} \right)\) đồng thời O là trung điểm của đoạn AB.

Từ giả thiết \(\overrightarrow {DM} = 3\overrightarrow {MC} \Rightarrow M\) là điểm thuộc đoạn CD và \(CM = \frac{1}{4}CD\)

Gọi \(\varphi \) là góc giữa đường thẳng SM và mặt phẳng \(\left( {SBC} \right)\) và \(N = OM \cap BC\).

\( \Rightarrow \sin \varphi = \frac{{d\left( {M,\left( {SBC} \right)} \right)}}{{SM}}\).

Ta có \(\frac{{d\left( {M,\left( {SBC} \right)} \right)}}{{d\left( {O,\left( {SBC} \right)} \right)}} = \frac{{MN}}{{ON}} = \frac{{CM}}{{BO}} = \frac{1}{2} \Rightarrow d\left( {M,\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {O,\left( {SBC} \right)} \right)\).

Kẻ \(OH \bot SB,\,\,H \in SB\).

Ta có \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot OH\).

Có \(\left\{ \begin{array}{l}OH \bot SM\\OH \bot BC\end{array} \right. \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\).

Trong tam giác vuông SOM ta có \(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{B^2}}} \Rightarrow OH = \frac{{SO.OB}}{{\sqrt {S{O^2} + O{B^2}} }} = \frac{{\sqrt 3 }}{4}a\).

\( \Rightarrow d\left( {M,\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {O,\left( {SBC} \right)} \right) = \frac{{\sqrt 3 }}{8}a\).

Vì CM là đường trung bình của tam giác BON nên

\(OM = \frac{1}{2}ON = \frac{1}{2}\sqrt {B{O^2} + B{N^2}} = \frac{1}{2}\sqrt {\frac{{{a^2}}}{4} + 4{a^2}} = \frac{{\sqrt {17} }}{4}a\)

\( \Rightarrow SM = \sqrt {S{O^2} + O{M^2}} = \frac{{\sqrt {29} }}{4}\)

\( \Rightarrow \sin \varphi = \frac{{d\left( {M,\left( {SBC} \right)} \right)}}{{SM}} = \frac{{\sqrt {87} }}{{58}}\)