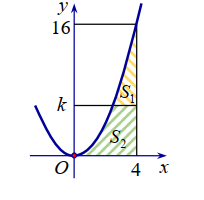
Cho hình phẳng giới hạn bởi các đường\(y=x^{2}, y=0, x=0, x=4\) . Đường thẳng \(y=k(0<k<16)\) chia  hình thành hai  phần có diện tích \(S_{1}, S_{2}\) , (hình vẽ). Tìm k để \(S_{1}=S_{2}\)

Tính tích phân sau: \(\mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} \sin \;3x.\cos \;xdx\)

Cho hình (H ) giới hạn bởi các đường\(y=-x^{2}+2 x\) trục hoành. Quay hình phẳng (H ) quanh trục Ox ta được khối tròn xoay có thể tích là:

Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}} {{x^2} - x}&{{\rm{ khi }}x \ge 0}\\ x&{{\rm{ khi }}x < 0} \end{array}} \right.\). Khi đó \(I=2\int\limits_{0}^{\frac{\pi }{2}}{\cos xf\left( \sin x \right)}dx+2\int\limits_{0}^{2}{f\left( 3-2x \right)}dx\) bằng

Biết \(I = \mathop \smallint \nolimits_0^1 \frac{x}{{4 - {x^2}}}dx =  - \frac{1}{2}\ln \frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản và a,b>0a,b>0 thì a2−ba2-b bằng  

Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiabg2 % da9maapehabaGaaG4maiaadIhacaGGUaGaamyzamaaCaaaleqabaGa % aGOmaiaadIhaaaGccaqGKbGaamiEaaWcbaGaaGimaaqaaiaaigdaa0 % Gaey4kIipaaaa!42D0! I = \int\limits_0^1 {3x.{e^{2x}}{\rm{d}}x} \)

Tính tích phân sau \(\mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} \left( {2\cos \;x - \sin \;2x} \right)dx\)

Giá trị của tích phân \(I=\int^{\ln 2}_0 \sqrt{e^{x}-1} d x\) là

Cho hàm số f liên tục trên đoạn [0;3]. Nếu \(\int_{0}^{3} f(x) d x=2\) thì tích phân \(\int_{0}^{3}[x-2 f(x)] d x\) có giá trị bằng

Giá trị của tích phân \(I=\int\limits_{0}^{\frac{\pi}{2}}\left(\sin ^{4} x+\cos ^{4} x\right)\left(\sin ^{6} x+\cos ^{6} x\right) d x\) là

Xét hàm số f liên tục trên R và các số thực a, b, c tùy ý. Trong các khẳng định sau, khẳng định nào sai?

Để tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamisaiabg2 % da9maapehabaGaamiEaiGacohacaGGPbGaaiOBaiaaykW7caaIXaGa % aGOmaiaadIhacaqGKbGaamiEaaWcbaGaaGimaaqaaiabec8aWbqdcq % GHRiI8aaaa!465F! H = \int\limits_0^\pi {x\sin \,12x{\rm{d}}x} \) bằng phương pháp tích phân từng phần ta đặt u = x  và dv = sin12xdx. Tìm  du và tính  H.

Diện tích hình phẳng giới hạn bởi đường cong \(y=x \ln x\), trục hoành và đường thẳng x=e là

Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa \(\int\limits_{ – 2}^2 {f\left( {\sqrt {{x^2} + 5} – x} \right){\rm{d}}x} = 1,\int\limits_1^5 {\frac{{f\left( x \right)}}{{{x^2}}}{\rm{d}}x} = 3.\) Tính \(\int\limits_1^5 {f\left( x \right){\rm{d}}x} .\)

Cho hàm số f(x) liên tục trên R và f(2) = 16, \(\mathop \smallint \nolimits_0^2 f\left( x \right)dx\; = \;4\). Tính \(\mathop \smallint \nolimits_0^1 xf'\left( {2x} \right)dx\)

Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ {\frac{1}{2}} \right\}\) thỏa mãn \(f’\left( x \right) = \frac{2}{{2x – 1}}\) và \(f\left( 0 \right) = 1,\,\,f\left( 1 \right) = 2\). Giá trị của biểu thức \(f\left( { – 1} \right) + f\left( 3 \right)\) bằng

Cho số hữu tỷ dương m thỏa mãn \(\int\limits_{0}^{\frac{\pi}{2 m}} x \cdot \cos m x d x=\frac{\pi-2}{2}\).Hỏi số m thuộc khoảng nào trong các khoảng dưới đây?

Giả sử là hàm số f(x) liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng  K. Khẳng định nào sau đây sai?

Cho hàm số f(x) liên tục trên ℝ và thỏa mãn\(f(1+2 x)+f(1-2 x)=\frac{x^{2}}{x^{2}+1}, \forall x \in \mathbb{R}\) . Tính tích phân \(I=\int_{-1}^{3} f(x) d x\)

Nếu \(\int_{-2}^{0}\left(5-e^{-x}\right) d x=K-e^{2}\) thì giá trị của K là:
 

Diện tích hình phẳng giới hạn bởi các đường \(y=x^{2}+2, x=1, x=2, y=0\)