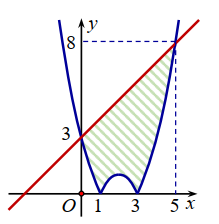
Cho hình phẳng (H ) giới hạn bởi các đường \(y=\left|x^{2}-4 x+3\right|, y=x+3\) (phần tô đậm trong hình vẽ). Diện tích của (H ) bằng

Câu hỏi liên quan

• Diện tích hình phẳng giới hạn bởi ay = x₂ và ax = y₂ là:

• Giá trị của \(\int\limits_0^2 {2{e^{2x}}{\rm{d}}x} \) là:

• Cho hàm số f(x) thỏa mãn \(f^{\prime}(x)+2 x \cdot f(x)=\mathrm{e}^{x} f(x) \text { với } f(x) \neq 0, \forall x \text { và } f(0)=1\)  . Khi đó \(\mid f(1)|\) bằng?

ZUNIA12

• Tính  tích phân sau \(I = \mathop \smallint \nolimits_0^{\frac{{\rm{\pi }}}{2}} \frac{{{e^x}.\sin x}}{{1 + \sin 2x}}dx\)

• Cho \(I=\int_{0}^{\frac{\pi}{2}} \frac{\cos 2 x}{1+2 \sin 2 x} d x=\frac{1}{4} \ln 3\) Tìm giá trị của a là:
   

• Tích phân \(\int_{2}^{3} \frac{x^{2}-x+4}{x+1} d x\) bằng
   

•  Cho hàm số f (x) có đạo hàm và đồng biến trên ℝ thỏa mãn \(f(0)=1 \text { và }\left(f^{\prime}(x)\right)^{2}=e^{x} f(x), \forall x \in \mathbb{R}\) . Tính tích phân \(\int_{0}^{1} f(x) d x\) bằng?

•  Biết \(\mathop \smallint \nolimits_0^1 \frac{{x + 2}}{{{x^2} + 4x + 7}}dx = a\ln \sqrt {12}  + b\ln \sqrt 7 \), với a, b là các số nguyên. Tổng  a + b là :

• Cho (H ) là hình phẳng giới hạn bởi các đường\(y=\sqrt{2 x} ; y=2 x-2\) và trục hoành. Tính diện tích của (H ) .

• Số nghiệm nguyên âm của phương trình \(x^{3}-a x+2=0 \text { với } a=\int_{1}^{3 e} \frac{1}{x} d x\) là:

• Cho hàm số \(f(x) = \left\{ \begin{array}{l} 1 - {x^2}\,\,\,\,{\rm{khi}}\;x \le 3\\ 7 - 5x\,\,\,{\rm{khi}}\,\,x > 3 \end{array} \right.\). Tính tích phân \(\int\limits_{0}^{\ln 2}{f\left( 3{{e}^{x}}-1 \right)}{{\text{e}}^{x}}\text{d}x\).

• Giá trị của tích phân \(\int\limits_{0}^{1}(2 x+1)^{5} d x\) là

• Biết \(\int_{0}^{1} \frac{2 x^{2}+3 x+3}{x^{2}+2 x+1} \mathrm{d} x=a-\ln b \text { vói } a, b\) là các số nguyên dương. Tính \(P=a^{2}+b^{2}\)

• Trong hệ trục tọa độ Oxy cho elip (E) có phương trình \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)Hình phẳng (H ) giới hạn bởi nửa elip nằm trên trục hoành và trục hoành. Quay hình (H ) xung quanh trục Ox ta được khối tròn xoay, tính thể tích khối tròn xoay đó:

• Cho \(I=\int_{1}^{e} x \ln x \mathrm{d} x=\frac{a \cdot \mathrm{e}^{2}+b}{c} \text { với } a, b, c \in \mathbb{Z}\). Tính T=a+b+c

• Trong các phép tính sau đây, phép tính nào sai?

• Kết quả \(I=\int_{0}^{1} \frac{x}{x+1} d x\) là 

• Cho hình (H ) giới hạn bởi các đường\(y=-x^{2}+2 x\) trục hoành. Quay hình phẳng (H ) quanh trục Ox ta được khối tròn xoay có thể tích là:

• Giả sử \(I = \mathop \smallint \nolimits_{ - 1}^0 \frac{{3{x^2} + 5x - 1}}{{x - 2}}dx = a\ln \frac{2}{3} + b\). Khi đó giá trị a + 2b là

• Tích phân \(I=\int_{0}^{1} \frac{x^{5} d x}{\left(1+x^{2}\right)^{3}}\) được kết quả\(I=a \ln 2-b\) . Giá trị a+b là