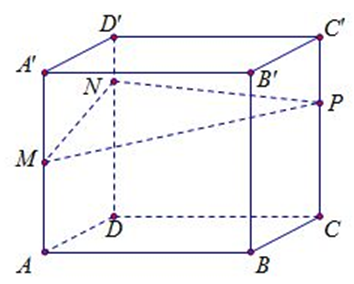
Cho khối hộp \(ABCD.A'B'C'D'\) có cạnh bên bằng 1; đáy \(ABCD\) là một hình chữ nhật có các cạnh \(BA=\sqrt{3},AD=\sqrt{7};\) các mặt  bên \(\left( ABB'A' \right)\) và \(\left( ADD'A' \right)\) hợp với mặt đáy các góc theo thứ tự \({{45}^{0}};{{60}^{0}}.\) Thể tích khối hộp là:

Câu hỏi liên quan

• Một khối lăng trụ tam giác có các cạnh đáy bằng 13, 14, 15, cạnh bên tạo với mặt phẳng đáy một góc 300 và có chiều dài bằng 8. Khi đó thể tích khối lăng trụ là

• Cho hình chóp S ABCD . có đáy là hình vuông tâm O, BD =1. Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy (ABCD) là trung điểm OD. Đường thẳng SD tạo với mặt phẳng đáy một góc 60⁰ Thể tích của khối chóp đã cho bằng

• Cho hình lăng trụ tứ giác ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a và thể tích bằng 3a3. Tính chiều cao h của hình lăng trụ đã cho.

ZUNIA12

• Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết \(SA \bot (ABCD);\,\,SA = a\sqrt 3 .\) Tính thể tích của khối chóp.

• Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên bằng 3a. Tính thể tích V của khối chóp đã cho.

• Thể tích khối lăng trụ tam giác đều có tất cả các cạnh đều bằng a là

• Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=3a, BC=4a và AB ⊥ (SBC) . Biết SB = \(2a\sqrt 3 \) và \(\widehat {SBC} = {30^0}\). Thể tích khối chóp S.ABC bằng:

• Thể tích của khối lăng trụ có khoảng cách giữa một đường thẳng bất kì của đáy này tới một đường thẳng bất kì của đáy kia bằng h và diện tích đáy bằng B là

• Tính thể tích V của khối lăng trụ tam giác đều có tất cả các cạnh bằng a.

• Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Thể tích của khối chóp đã cho bằng

• Cho khối hộp chữ nhật ABCD.A'B'C'D' có thể tích bằng 2110. Biết A'M = MA; DN = 3ND'D; CP = 2PC'. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằn

  

• Cho hình lăng trụ ABC.A’B’C’ vì M là trung điểm của CC’. Gọi khối đa diện (H) là phần còn lại của khối lăng trụ ABC.A’B’C’ sau khi cắt bỏ đi khối chóp M.ABC. Tính tỷ số thể tích của (H) và khối chóp M.ABC.

• Cho tứ diện \(ABCD.\) Gọi B’ và C’ lần lượt thuộc các cạnh AB và AC thỏa \(3AB'=AB\) và \(3AC'=AC\). Khi đó tỉ số thể tích của hai khối tứ diện \(k=\frac{{{V}_{AB'C'D}}}{{{V}_{ABCD}}}\) bằng:

• Cho hình chóp S.ABCD có thể tích bằng 48 và ABCD là hình thoi. Các điểm M, N, P, Q lần lượt là các điểm trên các đoạn SA, SB, SC, SD thỏa mãn: \(SA=2SM,SB=3SN;\) \(SC=4SP;SD=5SQ\). Tính thể tích khối chóp S.MNPQ

• Cho lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông cân tại B và AC = 2a biết rằng (A'BC) hợp với đáy (ABC) một góc 45^o.Thể tích lăng tru là:

• Cho hình chóp S.ABC có đáy là \(\Delta ABC\) vuông cân ở B, \(AC=a\sqrt{2},SA=a\) và \(SA\bot \left( ABC \right)\). Gọi G là trọng tâm của \(\Delta SBC\), một mặt phẳng \(\left( \alpha  \right)\) đi qua AG và song song vsơi BC cắt SC, SB lần lượt tại M, N. Thể tích khối chóp S.AMN bằng

• Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC = 2a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm H của cạnh AB và AA' = \(a\sqrt 2 \). Tính thể tích khối lăng trụ ABC.A'B'C' theo a.

   

• Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh bằng a, mặt bên \(SAB\) là tam giác đều, \(SC=SD=a\sqrt{3}.\) Tính thể tích khối chóp \(S.ABCD.\)

• Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A’BCD’) bằng \(\frac{a\sqrt{3}}{2}\). Tính thể tích hình hộp theo a.

• Khối lập phương ABCD.A’B’C’D’ có thể tích bằng \({{a}^{3}}\). Tính độ dài của A’C.