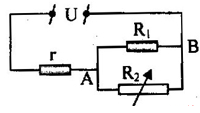
Cho mạch điện như hình vẽ:
Biết \(r = 3\Omega, R_1,R_2\) là một biến trở. U = 12V. Điều chỉnh biến trở R2 để cho công suất trên nó là lớn nhất, khi đó công suất trên R2 bằng 3 lần công suất R1. Tìm R1
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiVậy công suất cực đại trên R2 là: Ta có: \(rnt[R_1//R_2]\)
\( {R_{AB}} = \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\)
⇒ Điện trở toàn mạch: \( R = r + {R_{AB}} = r + \frac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \frac{{{R_2}(r + {R_1}) + r{R_1}}}{{{R_1} + {R_2}}}\)
+ Dòng điện mạch chính: \( I = \frac{U}{R} = \frac{{U({R_1} + {R_2})}}{{{R_2}(r + {R_1}) + r{R_1}}}\)
+ Từ hình vẽ, ta có: \( {U_2} = {U_{AB}} = I{R_{AB}} = \frac{{U{R_1}.{R_2}}}{{{R_2}(r + {R_1}) + r{R_1}}}\)
+ Công suất trên R2: \( {P_2} = \frac{{U_2^2}}{{{R_2}}} = \frac{{{U^2}R_1^2.{R_2}}}{{{{[{R_2}(r + {R_1}) + r{R_1}]}^2}}} = \frac{{{U^2}R_1^2}}{{{{[\sqrt {{R_2}} (r + {R_1}) + \frac{{r{R_1}}}{{\sqrt {{R_2}} }}]}^2}}}\)
+ Theo BDT Cosi ta có: \( \sqrt {{R_2}} (r + {R_1}) + \frac{{r{R_1}}}{{\sqrt {{R_2}} }} \ge 2\sqrt {(r + {R_1}){R_1}} \)
+ Vậy công suất cực đại trên R2 là: \( {P_2} = \frac{{{U^2}R_1^2}}{{4(r + {R_1})r{R_1}}} = \frac{{{U^2}{R_1}}}{{4(r + {R_1})r}}\)
+ Khi \(P_{2max}\) thì \( \sqrt {{R_2}} (r + {R_1}) = \frac{{r{R_1}}}{{\sqrt {{R_2}} }} \to {R_2} = \frac{{r{R_1}}}{{(r + {R_1})}} \to {R_2} = \frac{{3{R_1}}}{{(3 + {R_1})}}(1)\)
+ Mặt khác, theo đầu bào ta có: \( \frac{{{P_1}}}{{{P_2}}} = \frac{1}{3} \Leftrightarrow \frac{{\frac{{U_{AB}^2}}{{{R_1}}}}}{{\frac{{U_{AB}^2}}{{{R_2}}}}} = \frac{1}{3} \to \frac{{{R_2}}}{{{R_1}}} = \frac{1}{3} \to {R_1} = 3{R_2}(2)\)
Từ (1) và (2) giải ra ta có: \(\left\{ \begin{array}{l} {R_1} = 6\Omega \\ {R_2} = 2\Omega \end{array} \right.\)

.png)











