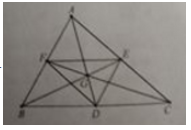
Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có: D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB
Do đó: DE, EF, FD là các đường trung bình của tam giác ABC
Suy ra \(\left\{ {\begin{array}{*{20}{l}} {FE\,\,{\rm{// = }}\frac{1}{2}BC}\\ {DE\,\,{\rm{// = }}\frac{1}{2}AB}\\ {DF\,\,{\rm{// = }}\frac{1}{2}AC} \end{array}} \right.\)
Do đó ta có các phép tịnh tiến như sau:
\( {T_{\frac{1}{2}\overrightarrow {BC} }}\left( F \right) = E;{T_{\overrightarrow {DE} }}\left( B \right) = F\)
Lại có G là trọng tâm tam giác ABC nên ta có DG = 1/2GA
\( {T_{\frac{1}{2}\overrightarrow {GA} }}\left( D \right) = G;{T_{2\overrightarrow {DG} }}\left( G \right) = A\)
Vậy đáp án A, B, D đúng và C sai.
Chọn đáp án C.