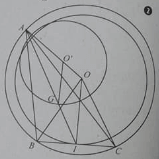
Cho tam giác ABC nội tiếp đường tròn (O;R). điểm A cố định, dây BC có độ dài bẳng R, G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu?

Câu hỏi liên quan

• Cho hai đường thẳng d và d’ cắt nhau. Có bao nhiêu phép vị tự biến d thành d’?

• Cho tam giác ABC nội tiếp đường tròn (O). BC cố định, I là trung điểm BC, G là trọng tâm của tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) là ảnh của (O) qua phép vị tự nào sau đây?

  

• Trong mặt phẳng tọa độ Oxy phép vị tự tâm H(1;-3) tỉ số k = 1/2, biến đường tròn (C) có phương trình : (x − 2)² + (y − 3)² = 32 thành đường tròn (C’) có phương trình:

ZUNIA12

• Trong mặt phẳng tọa độ Oxy cho phép vị tự tâm I (2;3) tỉ số k = -2 biến điểm M (-7;2) thành điểm M ' có tọa độ là:

• Trong mặt phẳng tọa độ Oxy cho đường thẳng \(\Delta: x+2 y-1=0\) và điểm I (1;0). Phép vị tự tâm I tỉ số k biến đường thẳng ∆ thành ∆' có phương trình là:

• Phép vị tự tâm O tỉ số -3 lần lượt biến hai điểm A, B thành hai điểm C, D. Mệnh đề nào sau đây đúng?

• Trong mặt phẳng tọa độ Oxy phép vị tự H(1;2) tỉ số k = -3 điểm M(4;7) biến thành điểm M’ có tọa độ

• Trong mặt phẳng Oxy cho đường tròn (C) có phương trình (x−1)²+(y−2)² = 4. Hỏi phép vị tự tâm O tỉ số k = -2 biến (C) thành đường tròn nào sau đây:

• Trong mặt phẳng tọa độ Oxy phép vị tự tâm O(0;0) tỉ số k = -5, biến đường thẳng d có phương trình : 2x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:

• Cho hai đường thẳng song song d và d ' và một điểm O không nằm trên chúng. Có bao nhiêu phép vị tự tâm O biến đường thẳng d thành đường thằng d ' ?

• Có bao nhiêu phép vị tự biến đường tròn (O; R) thành đường tròn (O; R') với \(R \neq R^{\prime} ?\)

• Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(0;2) tỉ số k = -1/2 , biến điểm M(12;-3) thành điểm M’ có tọa độ:

   

• Cho đường tròn (O; R). Có bao nhiêu phép vị tự biến (O; R) thành chính nó?

• Trong mặt phẳng Oxy, cho điểm A(2,−1). Ảnh của điểm A qua phép vị tự tâm O tỉ số k = 2 có tọa độ là: 

• Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;4) tỉ số k = -2, biến đường thẳng d có phương trình : 7x + 3y - 4 = 0 thành đường thẳng d’ có phương trình:

• Cho đường tròn (O; R ). Có bao nhiêu phép vị tự với tâm O biến (O;R ) thành chính nó?

• Cho hai đường tròn (O;R) và (O’;R) (O không trùng với O’). Có bao nhiều phép vị tự biến (O) thành (O’)?

• Cho hình thang ABCD có hai cạnh đáy là AB và CD thỏa mãn AB=3CD . Phép vị tự biến điểm A thành điểm C và biến điểm B thành điểm D có tỉ số k là:

• Cho hình thang ABCD , với  \(\overrightarrow{C D}=-\frac{1}{2} \overrightarrow{A B}\). Gọi I là giao điểm của hai đường chéo AC và BD . Xét phép vị tự tâm I tỉ số k biến \(\overrightarrow{A B}\) thành \(\overrightarrow{CD}\). Mệnh đề nào sau đây là đúng?
   

• Cho tứ diện ABCD có trọng tâm G. Phép vị tự tâm G biến mỗi đỉnh thành trọng tâm mặt đối diện có tỉ số vị tự là: