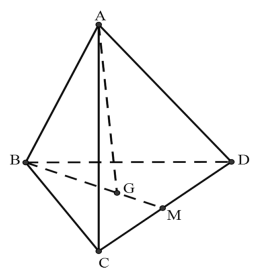
Cho tứ diện ABCD . Đặt \(\overrightarrow{A B}=\vec{a}, \overrightarrow{A C}=\vec{b}, \overrightarrow{A D}=\vec{c}\) gọi G là trọng tâm của tam giác BCD . Trong các đẳng thức sau, đẳng thức nào đúng?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiGọi M là trung điểm BC .
Khi đó
\(\begin{aligned} \vec{AG} &=\overrightarrow{A B}+\overrightarrow{B G}=\vec{a}+\frac{2}{3} \overrightarrow{B M}=\vec{a}+\frac{2}{3} \cdot \frac{1}{2}(\overrightarrow{B C}+\overrightarrow{B D}) \\ &=\vec{a}+\frac{1}{3}(\overrightarrow{A C}-\overrightarrow{A B}+\overrightarrow{A D}-\overrightarrow{A B})=\vec{a}+\frac{1}{3}(-2 \vec{a}+\vec{b}+\vec{c})=\frac{1}{3}(\vec{a}+\vec{b}+\vec{c}) \end{aligned}\)
ADMICRO
YOMEDIA
ZUNIA9
.png)