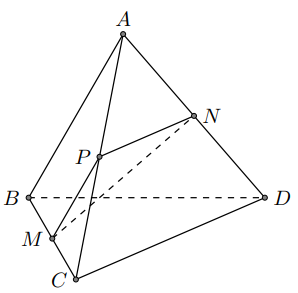
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và AD. Biết \(A B=C D=2 a, M N=a \sqrt{3}\). Tính góc giữa hai đường thẳng AB và CD
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
Gọi P là trung điểm AC \(\Rightarrow M P // A B, M P=\frac{1}{2} A B=a\text{ và }N P // C D, N P=\frac{1}{2} C D=a\)
\(\begin{aligned} &(A B, C D)=(P M, P N)\\ &\text { Ta có } \cos \widehat{M P N}=\frac{P M^{2}+P N^{2}-M N^{2}}{2 P M \cdot P N}=\frac{a^{2}+a^{2}-3 a^{2}}{2 a^{2}}=-\frac{1}{2} \text { . }\\ &\text { Từ đó suy ra } \widehat{M P N}=120^{\circ} \Rightarrow(A B, C D)=60^{\circ} \text { . } \end{aligned}\)
Câu hỏi liên quan
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Trong các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. \(SA \bot \left( {ABCD} \right)\), SA = x. Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60o.
-
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.
Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:
-
Mệnh đề nào sau đây là đúng?
-
Cho hình chóp S.ABC có hai mặt bên (SBC) và (SAC) vuông góc với đáy (ABC). Khẳng định nào sau đây sai?
-
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích của hình chóp S.ABCD là \(\frac{{{a}^{3}}\sqrt{15}}{6}\). Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là:
-
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, với AB = c, AC = b, cạnh bên AA' = h. Mặt phẳng (P) đi qua A' và vuông góc với B'C.Thiết diện của lăng trụ cắt bởi mặt phẳng (P) có hình:
.png)
-
Cho hình hộp ABCD.A'B'C'D' có AB = a, BC = b, CC' = c. Nếu \(AC' = BD' = B'D = \sqrt {{a^2} + {b^2} + {c^2}} \) thì hình hộp là
-
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc \(\widehat A = {60^0}\), cạnh \(SC = \frac{{a\sqrt 6 }}{2}\) và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SCA kẻ \(IK \bot SA\) tại K. Tính độ dài IK được
-
Trong các mệnh đề sau đây, mệnh đề nào là đúng?
-
Trong lăng trụ đều, khẳng định nào sau đây sai?
-
Cho hình chóp S.ABCD, đáy ABCD là hình vuông, \(SA \bot (ABCD)\). Gọi \((\alpha)\) là mặt phẳng chứa AB và vuông góc với (SCD), \((\alpha)\) cắt chóp S.ABCD theo thiết diện là hình gì?
-
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng a và góc \(\widehat A = {60^0}\), cạnh \(SC = \frac{{a\sqrt 6 }}{2}\) và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SAC kẻ \(IK \bot SA\) tại K. Tính số đo góc \(\widehat {{\rm{BKD}}}\).
-
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng A và góc \(\hat{A}=60^{\circ}\) , cạnh \(S C=\frac{a \sqrt{6}}{2}\) và SC vuông góc với mặt phẳng \((A B C D)\) . Trong tam giác SAC kẻ \(I K \perp S A\) tại K . Tính số đo góc \(\widehat{\mathrm{BKD}}\)
-
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và đáy ABC là tam giác cân ở A. Gọi H là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây đúng?
-
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (B C D). Biết tam giác BCD vuông tại C và \(A B=\frac{a \sqrt{6}}{2}, A C=a \sqrt{2}, C D=a\). Gọi E là trung điểm của AC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng A B và DE bằng
-
Cho các mệnh đề sau với \((\alpha) \text { và }(\beta)\) là hai mặt phẳng vuông góc với nhau với giao tuyến \(m=(\alpha) \cap(\beta) \) và a, b, c, d là các đường thẳng. Các mệnh đề sau, mệnh đề nào đúng?
-
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA = a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng bao nhiêu?
-
Cho ba tia Ox, Oy, Oz vuông góc nhau từng đôi một. Trên Ox, Oy, Oz lần lượt lấy các điểm A, B, C sao cho OA = OB = OC = a. Khẳng định nào sau đây sai?
