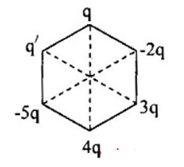
Đặt tại 6 đỉnh của lục giác đều các điện tích \(q, -2q, 3q, 4q, -5q; q'\). Xác định q' theo q để cường độ điện trường tại tâm O của lục giác bằng 0 biết q > 0.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
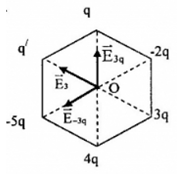
Báo saiGọi: + \( \overrightarrow {{E_{3q}}} \) là điện trường tổng hợp tại O do q và 4q gây ra. \( \overrightarrow {{E_{-3q}}} \) là điện trường tổng hợp tại O do −5q và −2q gây ra. \( \overrightarrow {{E_{3}}} \) là điện trường tổng hợp tại O do q và 4q gây ra.
Các véctơ được biểu diễn như hình.
Ta có: \( \overrightarrow {{E_0}} = \overrightarrow {{E_{ - 3q}}} + \overrightarrow {{E_{3q}}} + \overrightarrow {{E_3}} = \overrightarrow {{E_{ - 33}}} + \overrightarrow {{E_3}} \)
=> \( \overrightarrow {{E_{ - 33}}} \) cùng chiều \( \overrightarrow {{E_3}} \)
Ta có: \(\left\{ \begin{array}{l} {E_{ - 33}} = {E_3}\\ \overrightarrow E = \overrightarrow {{E_{ - 33}}} + \overrightarrow {{E_3}} \end{array} \right. \to E = 2{E_3} = 2k\frac{{3q}}{{{r^2}}} = k\frac{{6q}}{{{r^2}}}\)
Để tại O cường độ điện trường tổng hợp bằng 0 thì:
\(\overrightarrow {{E_{q'}}} + \overrightarrow E = 0 \to \left\{ \begin{array}{l} \overrightarrow {{E_{q'}}} \uparrow \downarrow \overrightarrow E \\ {E_{q'}} = E \Leftrightarrow k\frac{{\left| {q'} \right|}}{{{r^2}}} = k\frac{{6q}}{{{r^2}}} \to \left| {q'} \right| = 6q \end{array} \right. \to q' = 6q\)