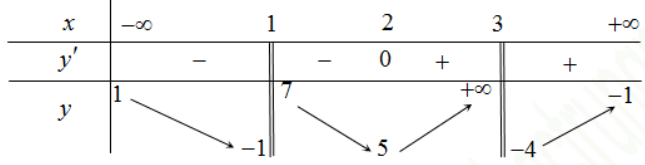Đồ thị hàm số \(y = \dfrac{{3x + \sqrt {{x^2} + 1} }}{{2 + \sqrt {3{x^2} + 2} }}\) có bao nhiêu đường tiệm cận ngang?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTXĐ: \(\mathbb{R}\).
Ta có:
+) \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{3 + \sqrt {1 + \dfrac{1}{{{x^2}}}} }}{{\dfrac{2}{x} + \sqrt {3 + \dfrac{2}{{{x^2}}}} }}\)\( = \dfrac{4}{{\sqrt 3 }} = \dfrac{{4\sqrt 3 }}{3}\)
+) \(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{3 - \sqrt {1 + \dfrac{1}{{{x^2}}}} }}{{\dfrac{2}{x} - \sqrt {3 + \dfrac{2}{{{x^2}}}} }}\)\( = - \dfrac{2}{{\sqrt 3 }} = - \dfrac{{2\sqrt 3 }}{3}\)
Suy ra đồ thị hàm số có các tiệm cận ngang: \(y = \dfrac{{4\sqrt 3 }}{3}\) và \(y = - \dfrac{{2\sqrt 3 }}{3}\).

.png)