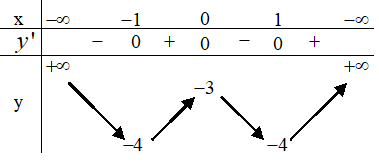
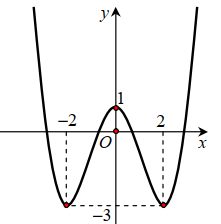
Đồ thị hàm số \(y = {x^3} - 3x\) cắt
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa xét từng phương án :
* Xét phương trình hoành độ giao điểm của và đường thẳng y = 3 :
\({x^3} - 3x = 3 \Rightarrow {x^3} - 3x - 3 = 0\)
Phương trình trên có 1 nghiệm duy nhất nên đồ thị cắt đường thẳng tại đúng 1 điểm.
* Xét phương trình hoành độ giao điểm của và đường thẳng y = -4 :
\({x^3} - 3x = - 4 \Rightarrow {x^3} - 3x + 4 = 0\)
Phương trình trên có 1 nghiệm duy nhất nên đồ thị cắt đường thẳng tại đúng 1 điểm.
* Xét phương trình hoành độ giao điểm của và đường thẳng y = 5/3
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
2{x^2} + {m^2} + 1 = 0\left( l \right)
\end{array} \right. \Leftrightarrow x = 0\)
Phương trình trên có 3 nghiệm nên đồ thị cắt đường thẳng tại 3 điểm.
* Xét phương trình hoành độ giao điểm của và trục hoành :
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
2{x^2} + {m^2} + 1 = 0\left( l \right)
\end{array} \right. \Leftrightarrow x = 0\)
Vậy đồ thị cắt trục hoành tại 3 điểm phân biệt.
Câu hỏi liên quan
-
Cho hàm số f có đạo hàm trên khoảng I. Xét các mệnh đề sau:
(I). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyyzImRaaGimaaaa!3BF1! f'\left( x \right) \ge 0\), \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeyiaIiIaam % iEaiabgIGiolaadMeaaaa!3A13! \forall x \in I\) (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I) thì hàm số đồng biến trên I.
(II). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0\),\(\forall x \in I\) (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I) thì hàm số nghịch biến trên I.
(III). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0; \forall x \in I\) thì hàm số nghịch biến trên khoảng I.
(IV). Nếu \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGabmOzayaafa % WaaeWaaeaacaWG4baacaGLOaGaayzkaaGaeyizImQaaGimaaaa!3BE0! f'\left( x \right) \le 0, \forall x \in I\) và f'(x) = 0 tại vô số điểm trên I thì hàm số f không thể nghịch biến trên khoảng I.
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
-
Đồ thị trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
-
Đồ thị hàm số \(y = {x^4} - 3{x^2} + ax + b\) có điểm cực tiểu A(2;−2). Tìm tổng (a+b)
-
Tất cả giá trị của tham số m để đồ thị hàm số \(\left( C \right):y = – 2{x^3} + 3{x^2} + 2m – 1\) cắt trục hoành tại ba điểm phân biệt là
-
Cho hàm số y=f(x) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị như hình bên. Đồ thị nào dưới đây là đồ thị của hàm số y=f(x)+1?
-
Đồ thị hàm số \(y = {x^2} – \left| x \right| + 1\) cắt trục tung tại điểm có tung độ bằng
-
Đồ thị hàm số nào dưới đây có tâm đối xứng là điểm \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysamaabm % aabaGaaGymaiaacUdacqGHsislcaaIYaaacaGLOaGaayzkaaaaaa!3B6E! I\left( {1; - 2} \right)\)?
-
Bảng biến thiên sau là của hàm số nào?
-
Hàm số y = 2x4 – (m2 – 4)x2 + 3 có 3 cực trị khi:
-
Đồ thị hàm số \(y = \sqrt {{{\sin }^2}x + 4} \) cắt trục tung tại điểm có tung độ bằng
-
Cho hàm số y = −x3 − 3x2 + 4 có đồ thị (C) là hình vẽ dưới đây. Với giá trị nào của mm thì phương trình x3 + 3x2 + m = 0(∗) có hai nghiệm phân biệt?
.png)
-
Với giá trị nào của mmthì đường thẳng y = −x + m cắt đồ thị hàm số \(\left( C \right):y = \frac{{x - 2}}{{1 - x}}\) tại hai điểm phân biệt là
-
Biết \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqamaabm % aabaGaamiEamaaBaaaleaacaWGbbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGbbaabeaaaOGaayjkaiaawMcaaaaa!3E80! A\left( {{x_A};\,{y_A}} \right)\),\(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)\) là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOqamaabm % aabaGaamiEamaaBaaaleaacaWGcbaabeaakiaacUdacaaMc8UaamyE % amaaBaaaleaacaWGcbaabeaaaOGaayjkaiaawMcaaaaa!3E83! B\left( {{x_B};\,{y_B}} \right)\) sao cho đoạn thẳng AB có độ dài nhỏ nhất. Tính \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiabg2 % da9iaadIhadaqhaaWcbaGaamyqaaqaaiaaikdaaaGccqGHRaWkcaWG % 4bWaa0baaSqaaiaadkeaaeaacaaIYaaaaOGaey4kaSIaamyEamaaBa % aaleaacaWGbbaabeaakiaac6cacaWG5bWaaSbaaSqaaiaadkeaaeqa % aaaa!439D! P = x_A^2 + x_B^2 + {y_A}.{y_B}\).
-
Cho hàm số \(:y = \frac{1}{3}{x^3} – m{x^2} – x + m + \frac{2}{3}\) có đồ thị \(\left( {{C_m}} \right)\). Tất cả các giá trị của tham số m để \(\left( {{C_m}} \right)\) cắt trục Ox tại ba điểm phân biệt có hoành độ \({x_1},{\rm{ }}{x_2},{\rm{ }}{x_3}\) thỏa \(x_1^2 + x_2^2 + x_3^2 > 15\) là
-
Cho hàm số \(% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyEaiabg2 % da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiabgkHiTiaa % dIhacqGHRaWkcaaIXaaabaGaamiEaiabgkHiTiaaigdaaaaaaa!4024! y = \frac{{{x^2} - x + 1}}{{x - 1}}\) có đồ thị (C). Gọi A,B là hai điểm phân biệt trên đồ thị (C) có hoành độ \(x_1;x_2\) thỏa \(x_1<1<x_2\). Giá trị nhỏ nhất của AB là
-
Tọa độ giao điểm giữa đồ thị \((C):y = \frac{{2x – 1}}{{x + 2}}\) và đường thẳng \(d:y = x – 2\) là
-
:Cho hàm số y=f(x) có bảng biến thiên như sau
Số nghiệm của phương trình \(f(2-x)-1=0\) là
-
Giao điểm giữa đồ thị \((C):y = \frac{{{x^2} – 2x – 3}}{{x – 1}}\) và đường thẳng \(\left( d \right):y = x + 1\) là
-
Đồ thị (C) của hàm số \(y = \frac{{2x - 8}}{x}\) cắt đường thẳng Δ: y = - x tại hai điểm phân biệt A và B. Tìm tọa độ trung điểm I của đoạn thẳng AB
-
Trong các đồ thị hàm số sau, đồ thị nào là đồ thị của hàm số \(y\; = \;\frac{x}{{\left| {x\; - \;1} \right|}}\) ?
