Dùng một hạt a có động năng 7,7 MeV bắn vào hạt nhân \(_{7}^{14}\text{N}\) đang đứng yên gây ra phản ứng \(\alpha +_{7}^{14}N\to _{1}^{1}p+_{8}^{17}O.\) Hạt prôtôn bay ra theo phương vuông góc với phương bay tới của hạt a. Cho khối lượng các hạt nhân:\({{m}_{\alpha }}=4,0015\text{ }u;\text{ }{{m}_{P}}=1,0073\text{ }u;\text{ }{{m}_{N}}=13,9992\text{ }u;{{m}_{O}}=16,9947\text{ }u.\) Biết 1u = 931,5 MeV/c2. Động năng của hạt nhân \(_{8}^{17}\text{O}\) là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiÁp dụng định luật bảo toàn động lượng, ta có:
\(\text{ }\overrightarrow{{{p}_{\alpha }}}=\overrightarrow{{{p}_{p}}}+\overrightarrow{{{p}_{O}}}\Rightarrow \overrightarrow{{{p}_{O}}}=\overrightarrow{{{p}_{\alpha }}}-\overrightarrow{{{p}_{p}}}\)
\(\Leftrightarrow p_{O}^{2}=p_{p}^{2}+p_{\alpha }^{2}-2.{{p}_{p}}.{{p}_{\alpha }}.cos\varphi\)
\(\Leftrightarrow {{m}_{O}}.{{K}_{O}}={{m}_{p}}.{{K}_{p}}+{{m}_{\alpha }}.{{K}_{\alpha }}-2.\sqrt{{{m}_{p}}.{{K}_{p}}}.\sqrt{{{m}_{\alpha }}.{{K}_{\alpha }}}.cos{{90}^{0}}\)
\(\Leftrightarrow {{K}_{O}}=\frac{{{m}_{p}}.{{K}_{p}}+{{m}_{\alpha }}.{{K}_{\alpha }}}{{{m}_{O}}}\)
\(\Leftrightarrow {{K}_{O}}=\frac{{{K}_{p}}+4,0015.7,7}{16,9947}\text{.}\)
Năng lượng của phản ứng hạt nhân:
\(\text{ }W={{K}_{O}}+{{K}_{p}}-{{K}_{\alpha }}=\left[ \left( {{m}_{\alpha }}+{{m}_{N}} \right)-\left( {{m}_{p}}+{{m}_{O}} \right) \right].{{c}^{2}}\)
\(\Leftrightarrow \frac{{{K}_{p}}+4,0015.7,7}{16,9947}+{{K}_{p}}-7,7=\left[ \left( 4,0015+13,9992 \right)-\left( 1,0073+16,9947 \right) \right].931,5\)
\(\Rightarrow \frac{{{K}_{p}}+4,0015.7,7}{16,9947}+{{K}_{p}}-7,7=-1,21095\)
\(\Rightarrow {{K}_{p}}=4,416\text{ MeV}\text{.}\)
Vậy \({{K}_{O}}=\frac{4,416+4,0015.7,7}{16,9947}=\text{2,073 MeV}\text{.}\)
Câu hỏi liên quan
-
Một hạt α có động năng 3,9 MeV đến đập vào hạt nhân \(_{13}^{27}Al\) đứng yên gây nên phản ửng hạt nhân \(\alpha + _{13}^{27}Al \to n + _{15}^{30}P\). Tính tổng động năng của các hạt sau phản ứng. Cho mα = 4,0015u; mn = l,0087u; nAl = 26,97345u; mp = 29,97005u; 1uc2 = 931 (MeV)
-
Các phản ứng hạt nhân không tuân theo các định luật nào?
-
Khi bắn phá hạt nhân \({}_{7}^{14}N\) bằng hạt \(\alpha ,\) người ta thu được một hạt prôton và một hạt nhân X. Hạt nhân X là
-
Năng lượng liên kết riêng của một hạt nhân được tính bằng:
-
Dùng một proton có động năng 5,58MeV bắn phá hạt nhân \( {}_{11}^{23}Na\) đứng yên, sinh ra hạt \(\alpha \) và hạt nhân X và không kèm theo bức xạ gamma. Biết năng lượng tỏa ra trong phản ứng chuyển hết thành đọng năng của các hạt tạo thành, động năng của hạt \(\alpha\) là 6,6MeV và động năng của hạt X là 2,648MeV. Cho khối lượng các hạt tính theo u bằng số khối. Góc tạo bởi hướng chuyển động của hạt \(\alpha\) và hướng chuyển động của hạt proton là
-
Năng lượng tối thiểu cần thiết để chia hạt nhân \(_{6}^{12}C\) thành 3 hạt α là bao nhiêu? (biết mC = 11,9967 u, mα = 4,0015 u).
-
Xét một phản ứng hạt nhân: \(_1^2H + _1^2H \to _2^3He + _0^1n\) . Biết khối lượng của các hạt nhân: mH = 2,0135u; mHe = 3,0149u; mn = l,0087u; 1u = 931 MeV/c2. Năng lượng phản ứng trên toả ra là
-
Cho phản ứng hạt nhaanm ban đầu hạt nhân Al đứng yên: \(_{2}^{4}He+_{13}^{27}Al\to _{15}^{30}P+_{0}^{1}n.\) Giả sử hai hạt tạo thành bay ra với cùng vận tốc và phản ứng không kèm bức xạ γ. Lấy khối lượng bằng số khối của chúng. Xác định động năng của hạt n, biết phản ứng thu năng lượng là 2,70 MeV.
-
Bắn hạt α có động năng 4 (MeV) vào hạt nhân nitơ đứng yên, xẩy ra phản ứng hạt nhân: \(\alpha + _7^{14}N \to _8^{17}O + p\) . Biết động năng của hạt prôtôn là 2,09 (MeV) và hạt prôtôn chuyển động theo hướng hợp với hướng chuyển động của hạt α một góc 60°. Coi khối lượng xấp xỉ bằng số khối. Xác định năng lượng của phản ứng tỏa ra hay thu vào.
-
Trong phản ứng vỡ hạt nhân urani U235 năng lượng trung bình toả ra khi phân chia một hạt nhân là 200 MeV. Khi 1 kg U235 phân hạch hoàn toàn thì toả ra năng lượng là
-
Trong chân không, một tia X và một tia hồng ngoại có bước sóng lần lượt là 0,2 nm và 820 nm. Tỉ số giữa năng lượng mỗi phôtôn của tia X và năng lượng mỗi phôtôn của tia hồng ngoại là
-
Dùng hạt α bắn phá hạt nhân nhôm (Al) đứng yên thu được hạt X và hạt notron. Cho khối lượng nghỉ của các hạt lần lượt là \( {m_\alpha } = 4,00150u,{m_{Al}} = 26,97435u,{m_\alpha } = 4,00150u,{m_{Al}} = 26,97435u,\). Năng lượng của phản ứng này tỏa ra hoặc thu vào là
-
Hạt nhân heli \(\left( _{2}^{4}He \right)\) có năng lượng liên kết là 28,4 MeV; hạt nhân liti \(\left( _{3}^{7}Li \right)\) có năng lượng liên kết là 39,2 MeV; hạt nhân đơtêri \(\left( _{1}^{2}D \right)\) có năng lượng liên kết là 2,24 MeV. Hãy sắp theo thứ tự tăng dần về tính bền vững của chúng
-
Dùng một proton có động năng 5,58 (MeV) bắn phá hạt nhân \(_{11}^{23}Na\) đứng yên sinh ra hạt α và hạt nhân X và không kèm theo bức xạ \(\gamma\). Biết năng lượng toả ra trong phản ứng chuyển hết thành động năng của các hạt tạo thành, động năng của hạt α là 6,6 (MeV) và động năng hạt X là 2,648 (MeV). Cho khối lượng các hạt tính theo u bằng số khối. Góc tạo bởi hướng chuyển động của hạt α và hướng chuyển động hạt proton là
-
Phản ứng hạt nhân thực chất là:
-
Hạt nhân
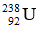đứng yên phân rã α thành hạt nhân 
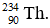Coi khối lượng hạt nhân tính theo đơn vị u bằng số khối. Hỏi động năng của hạt α bằng bao nhiêu % của năng lượng phân rã? -
Phản ứng hạt nhân không tuân theo:
-
Tìm phương án sai. Năng lượng liên kết hạt nhân bằng
-
Hạt α có động năng 6,3 (MeV) bắn vào một hạt nhân \(_4^9Be\) đứng yên, gây ra phản ứng: \(\alpha + _4^9Be \to _6^{12}C + n\). Cho biết phản ứng tỏa ra một năng lượng 5,7 (MeV), động năng của hạt C gấp 5 lần động năng hạt n. Động năng của hạt nhân n là
-
Dùng hạt α bắn phá hạt nhân nitơ đang đứng yên thì thu được một hạt prôtôn và hạt nhân ôxi theo phản ứng: \(_{2}^{4}\alpha +_{7}^{14}\text{N}\to _{8}^{17}\text{O}+_{1}^{1}\text{p}.\) Biết khối lượng các hạt trong phản ứng trên là: \({{\text{m}}_{\alpha }}=4,0015\text{ u}; {{\text{m}}_{\text{N}}}=13,9992\text{ u}; {{\text{m}}_{\text{O}}}=16,9947\text{ u}; {{\text{m}}_{\text{p}}}=1,0073\text{ u}.\) Nếu bỏ qua động năng của các hạt sinh ra thì động năng tối thiểu của hạt α là
