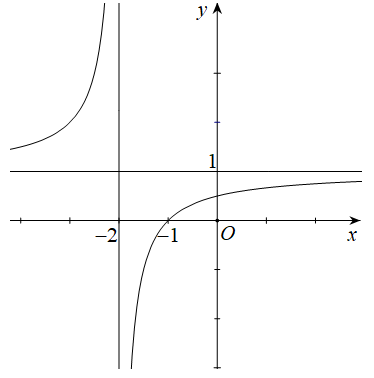
Hàm số y = 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình \(2{\left| x \right|^3} - 9{x^{2\;}}\; + \;12\left| x \right|\; + \;m\; = \;0\) có sáu nghiệm phân biệt.
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai+ Trước tiên từ đồ thị hàm số \({\left| x \right|^3}\; - \;9{x^2}\; + \;12\left| x \right|\), ta suy ra đồ thị hàm số \(y = 2{\left| x \right|^3}\; - \;9{x^2}\; + \;12\left| x \right|\) như hình dưới đây:
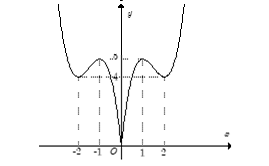
+ Phương trình \(2{\left| x \right|^3}\; - \;9{x^2}\; + \;12\left| x \right|\; + \;m\; = \;0\) và đường thẳng y = -m
+ Dựa vào đồ thị hàm số \(y=2{\left| x \right|^3}\; - \;9{x^2}\; + \;12\left| x \right|\), yêu cầu bài toán trở thành
\(4 < - m < 5 \Leftrightarrow - 5 < m < - 4\)
ADMICRO
YOMEDIA
ZUNIA9

.png)
.png)