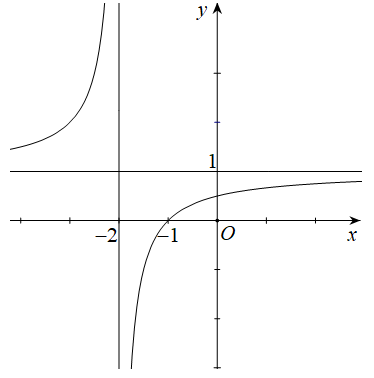
Cho hàm sốy=f(x) Hàm số \(y=f'(x)\) có đồ thị như hình vẽ bên dưới.
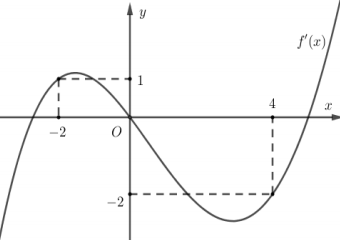
Có tất cả bao nhiêu giá trị nguyên \(m \in[-10 ; 10]\) đê hàm số \(g(x)=f( 1-2 x+m)+x^{2}-(m+1) x+m^{2}\) nghịch biến trên khoảng (1 ; 2)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai
\(\begin{array}{l} g^{\prime}(x)=-2 f^{\prime}(1-2 x+m)+2 x-m-1, \forall x \in \mathbb{R} \\ g^{\prime}(x) \leq 0 \Leftrightarrow f^{\prime}(1-2 x+m) \geq-\frac{1}{2} 1-2 x+m \Leftrightarrow\left[\begin{array}{c} 1-2 x+m \geq 4 \\ -2 \leq 1-2 x+m \leq 0 \end{array}\right. \\ \Leftrightarrow\left[\begin{array}{l} 1-2 x+m \geq 4 \\ -2 \leq 1-2 x+m \leq 0 \end{array} \Leftrightarrow\left[\begin{array}{l} x \leq \frac{m-3}{2} \\ \frac{1+m}{2} \leq x \leq \frac{3+m}{2} \end{array}\right.\right. \\ g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(1-2 x+m)=-\frac{1}{2} 1-2 x+m \Leftrightarrow x \in\left\{\frac{m-3}{2} ; \frac{1+m}{2} ; \frac{3+m}{2}\right\}: \text { hữu hạn. } \end{array}\)
Hàm số nghịch biến trên (1;2) \(\Leftrightarrow g^{\prime}(x) \leq 0, \forall x \in (1 ; 2)\)
\(\Leftrightarrow g^{\prime}(x) \leq 0, \forall x \in 1 ; 2 \Leftrightarrow\left[\begin{array}{l} 2 \leq \frac{m-3}{2} \\ \frac{1+m}{2} \leq 1<2 \leq \frac{3+m}{2} \end{array} \Leftrightarrow\left[\begin{array}{l} m \geq 7 \\ m=1 \end{array}\right.\right.\)
Vậy \(m\in \{1 ; 7 ; 8 ; 9\}\)
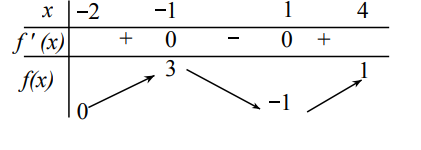
.png)
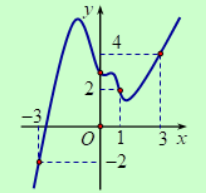
.png)