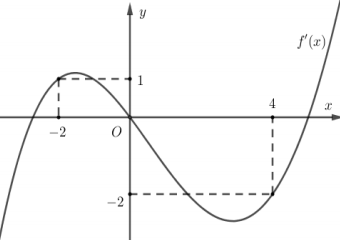
Cho hàm số f(x). Đồ thị y=f'(x) cho như hình bên. Hàm số \(g(x)=f(x-1)-\frac{x^{2}}{2}\) nghịch biến trong khoảng nào dưới đây
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai\(\begin{array}{l} \text { Ta có: } g(x)=f(x-1)-\frac{x^{2}}{2} \Rightarrow g^{\prime}(x)=f^{\prime}(x-1)-x \\ \Rightarrow g^{\prime}(x)=0 \Leftrightarrow f^{\prime}(x-1)-x=0 \Leftrightarrow f^{\prime}(x-1)=(x-1)+1 \end{array}\)
Đặt \(t=x-1 \text { thì } f^{\prime}(t)=t+1\)
Vẽ đường thẳng \(y=x+1 \) trên cùng một hệ trục tọa độ với đồ thị hàm số \(y=f^{\prime}(x)\) (như hình vẽ bên).
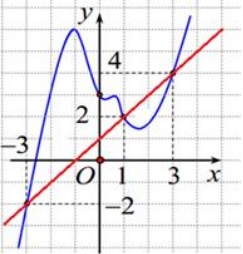
Dựa vào đồ thị \(f^{\prime}(t)=t+1 \Leftrightarrow t=-3, t=1, t=3\)
Hàm số nghịch biến \(g^{\prime}(x)=f^{\prime}(x-1)-x \leq 0 \Leftrightarrow f^{\prime}(t) \leq t \Leftrightarrow t \in(-\infty ;-3) \cup(1 ; 3)\)
Do đó \(x \in(-\infty ;-2) \cup(2 ; 4)\) vậy g(x) nghịch biến trên (2;4).
.png)