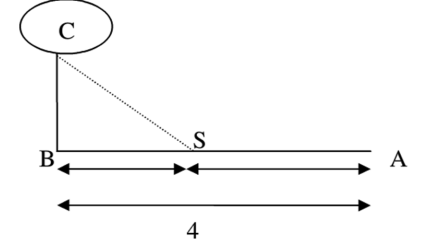
Hàm số \(y = 4\sqrt {{x^2} - 2x + 3} + 2x - {x^2}\) đạt giá trị lớn nhất tại hai giá trị x mà tích của chúng là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTXĐ: D = R
Ta có:
\(\begin{array}{l}
y' = \frac{{4\left( {x - 1} \right)}}{{\sqrt {{x^2} - 2x + 3} }} - 2x + 2\\
y' = 0 \Leftrightarrow \frac{{4\left( {x - 1} \right)}}{{\sqrt {{x^2} - 2x + 3} }} - 2x + 2 = 0\\
\Leftrightarrow \frac{{2\left( {x - 1} \right)\left( {2 - \sqrt {{x^2} - 2x + 3} } \right)}}{{\sqrt {{x^2} - 2x + 3} }} = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 1\\
\sqrt {{x^2} - 2x + 3} = 2
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x = 1 \pm \sqrt 2
\end{array} \right.
\end{array}\)
BBT
Do đó hàm số đạt GTLN tại \({x_{1,2}} = 1 \pm \sqrt 2 \)
Vậy \({x_1}.{x_2} = - 1\)
.png)