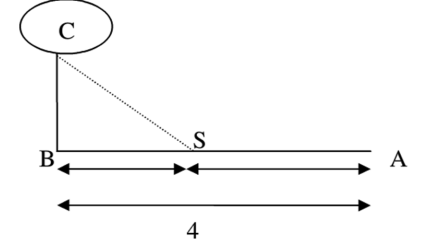
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C khoảng cách ngắn nhất từ C đến B là 1 km . Khoảng cách từ B đến A là 4 . Mỗi km dây điện đặt dưới nước là mất 5000 USD , còn đặt dưới đất mất 3000 USD . Hỏi điểm S trên bờ cách A bao nhiêu để khi mắc dây điện từ A qua S rồi đến C là ít tốn kém nhất?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi x là khoảng cách từ A đến S \((0 \leq x \leq 4)\) ,
ta có \(B S=4-x, C S=\sqrt{(4-x)^{2}+1}=\sqrt{x^{2}-8 x+17}\) .
Chi phí cho đường dây diện là \(y=3000 x+5000 \sqrt{x^{2}-8 x+17}\) .
Muốn ít tốn kém chi phí nhất ta cần tìm x để \(y_{\min }\) .
Xét hàm số \(y=3000 x+5000 \sqrt{x^{2}-8 x+17} \text { với } x \in[0,4]\).
Ta có
\(y^{\prime}=3000+\frac{5000(2 x-8)}{2 \sqrt{x^{2}-8 x+17}}=\frac{1000\left(3 \sqrt{x^{2}-8 x+17}+5 x-20\right)}{\sqrt{x^{2}-8 x+17}}\)
\(y^{\prime}=0 \Leftrightarrow 3 \sqrt{x^{2}-8 x+17}=20-5 x\)
\(\Leftrightarrow\left\{\begin{array}{l} x \leq 4 \\ 9 x^{2}-72 x+153=400-200 x+25 x^{2} \end{array} \Leftrightarrow\left\{\begin{array}{l} x \leq 4 \\ 16 x^{2}-128 x+247=0 \end{array}\right.\right.\)
\(\Leftrightarrow\left\{\begin{array}{l} x \leq 4 \\ x=\frac{19}{4}(\text { loại }) \\ x=\frac{13}{4}(\text { nhận }) \end{array}\right.\)
Mà \(y(0)=5000 \sqrt{17}, y(4)=17000, y\left(\frac{13}{4}\right)=16000\)
Suy ra \(\min _{[0,4]} y=16000 \text { khi } x=\frac{13}{4} \mathrm{km}\)
Câu hỏi liên quan
-
Giá trị lớn nhất của hàm số \(f(x)=\frac{\ln x}{x}\) trên đoạn [1;3] là:
-
\(\text{Tìm giá trị nhỏ nhất của hàm số }y = f\left( x \right) = \frac{{11x - 1}}{{2x + 3}}\text{ trên đoạn } \left[ {2;6} \right]\)
-
Xét hàm số \(y = \left| {{x^2} + ax + b} \right|\), với a,b là tham số. Gọi M là giá trị lớn nhất của hàm số trên \(\left[ { – 1;3} \right]\). Khi M nhận giá trị nhỏ nhất có thể được, tính a + 2b.
-
Tìm M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số \(y=x+\sqrt{2} \cos x\) trên đoạn \(\left[0 ; \frac{\pi}{2}\right]\).
-
Gọi m là giá trị để hàm số \(y = \frac{{x – {m^2}}}{{x + 8}}\) có giá trị nhỏ nhất trên \(\left[ {0;\;3} \right]\) bằng – 2. Mệnh đề nào sau đây là đúng?
-
Giá trị nhỏ nhất của hàm số \(y=e^{x}\left(x^{2}-3\right)\) trên đoạn [-2;2]
-
Hằng ngày, mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (mét) của mực nước trong kênh tính theo thời gian t (giờ) trong một ngày, \(0≤t≤24\)
-
Cho hàm số \(y=\frac{2 \cos ^{2} x+|\cos x|+1}{|\cos x|+1}\). Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số đã cho. Khi đó M+m bằng
-
Gọi M là giá trị lớn nhất của hàm số \(\begin{equation} f(x)=\left|3 x^{4}-4 x^{3}-12 x^{2}+m\right| \end{equation}\) trên đoạn [-1;3]. Có bao nhiêu số thực m để \(\begin{equation} M=\frac{59}{2} ? \end{equation}\)
-
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{{{x^2} + mx + m}}{{x + 1}}} \right|\) trên \(\left[ {1;\,2} \right]\) bằng 2. Số phần tử của S là
-
Hàm số\(y=\sqrt{1+x}+\sqrt{1-x}\) có giá trị lớn nhất, giá trị nhỏ nhất lần lượt là:
-
Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số \(y = \frac{{x – {m^2} – 2}}{{x – m}}\) trên đoạn \(\left[ {0;4} \right]\) bằng – 1.
-
Giá trị lớn nhất của hàm số \(y=2 \sin x-\frac{4}{3} \sin ^{3} x \text { trên }[0 ; \pi]\) là:
-
Cho hàm số y = f(x) có bảng biến thiên như sau:
.png)
Tất cả các giá trị của m để bất phương trình \(f\left( {\sqrt {x – 1} + 1} \right) \le m\) có nghiệm là
-
Tính giá trị nhỏ nhất của hàm số \(y=x+\frac{4}{x+1}\)trên đoạn [0; 4]
-
Cho hàm số y =f(x) có bảng biến thiên như sau:
.PNG)
Khẳng định nào sau đây đúng?
-
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên dưới. Biết rằng m và n là hai tham số thực. Để hàm số \(g\left( x \right) = 3f\left( {3x – m} \right) + f\left( {x + n} \right) – {x^2} + 4x\) đạt giá trị lớn nhất thì P = 2m – n bằng:
.jpg.png)
-
Cho hàm số \(f(x)=\sin ^{3} x-3 \sin x+2 .\) Gọi và lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho.
Khi đó là \(M+2 m\) là? -
Hàm số \(y=x+\frac{1}{x}+x^{2}+\frac{1}{x^{2}}\) có giá trị nhỏ nhất, giá trị lớn nhất trên đoạn [1;3] là:
-
Hàm số \(y=(x-1)(x-2)(x-3)(x-4)\) có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn [-1; 3] là:
