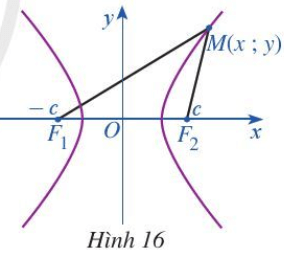
Lấy một tấm bìa, trên đó đánh dấu hai điểm F1 và F2. Lấy một cây thước thẳng với mép thước AB có chiều dài d và một đoạn dây không đàn hồi có chiều dài l sao cho d – l = 2a nhỏ hơn khoảng cách F1F2 (Hình 6a). Đính một đầu dây vào đầu A của thước nhưng đổi chỗ cố định đầu dây còn lại vào F1, đầu B của thước trùng với F2 sao cho đoạn thẳng BA có thể quay quanh F2 và làm tương tự như lần đầu để đầu bút chì M vẽ được một nhánh khác của đường H (Hình 6c). Tính MF2 – MF1

Cho elip \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Trong các khẳng định sau, khẳng định nào sai?

Elip \(\left( E \right):\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{{12}} = 1\) có một đỉnh nằm trên trục bé là:

Cho đường tròn có phương trình \(x^{2}+y^{2}+5 x-4 y+4=0\) . Tâm của đường tròn có tọa độ là 

Elip \((E): \frac{x^{2}}{100}+\frac{y^{2}}{64}=1\) có độ dài trục bé bằng: 

Elip có tổng độ dài hai trục bằng 18 và tỉ số của tiêu cự với độ dài trục lớn bằng \(\frac{3}{5}\). Phương trình chính tắc của elip là: 

Elip  \((\mathrm{E}): \frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)có tâm sai bằng bao nhiêu? 

Trong mặt phẳng, xét đường hypebol (H) là tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a, ở đó F₁F₂ = 2c với c > a > 0. Ta chọn hệ trục toạ độ Oxy có gốc là trung điểm của đoạn thẳng F₁F₂. Trục Oy là đường trung trực của F₁F₂ và F₂ nằm trên tia Ox (Hình 16). Khi đó F₁(c; 0), F₂(c; 0) là các tiêu điểm của (H).

Với mỗi điểm M(x; y) thuộc đường hypebol (H). Tính MF₁² theo x, y ta được:

Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm (1 dặm \( \approx 1,609km\)). Tìm tâm sai của quỹ đạo đó biết bán kính của Trái Đất xấp xỉ 4000 dặm.

Trong mặt phẳng tọa độ Oxy, ta xét parabol (P) có phương trình chính tắc y² = 2px (p > 0) (Hình 19).

Toạ độ tiêu điểm F của parabol (P) bằng:

Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{1} = 1\). Toạ độ các đỉnh, tiêu điểm, tiêu cự của hypebol lần lượt là:

Đường tròn \(x^{2}+y^{2}+\frac{x}{\sqrt{2}}-\sqrt{3}=0\) có tâm là điểm nào trong các điể sau đây? 

Elip (E) có độ dài trục bé bằng tiêu cự. Tỉ số e của tiêu cự với độ dài trục lớn của (E) bằng bao nhiêu?

Một nhà vòm chứa máy bay có mặt cắt hình nửa elip cao 8m, rộng 20m (Hình 16). Chọn hệ tọa độ thích hợp. Khoảng cách theo phương thẳng đứng từ một điểm cách chân tường 5m lên nóc nhà vòm là:

Tâm đường tròn \(x^{2}+y^{2}-10 x+1=0\) cách trục Oy một khoảng bằng?

Để vẽ hypebol (H) bạn An đã thực hiện các bước như sau:

Vẽ hypebol (H) với a = 3, b = 4. (H) có các đỉnh là A₁(– 3; 0), A₂(3; 0).

Bước 1. Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng x = –3, x = 3, y = – 4, y = 4.

Bước 2. Vẽ hai đường chéo của hình chữ nhật cơ sở.

Tim một số điểm cụ thể thuộc hypebol, chẳng hạn ta thấy điểm\(M\left( {5;\frac{{16}}{3}} \right)\) thuộc (H). Do đó các điểm\({M_1}\left( {5; - \frac{{16}}{3}} \right),{M_2}\left( { - 5;\frac{{16}}{3}} \right),{M_3}\left( { - 5; - \frac{{16}}{3}} \right)\) thuộc (H).

Bước 3. Vẽ đường hypebol bên ngoài hình chữ nhật cơ sở; nhánh bên trái tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm A₁(– 3; 0) và đi qua M₂, M₃; nhánh bên phải tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm A₂(3; 0) và đi qua M, M₁. Vẽ các điểm thuộc hypebol càng xa gốc toạ độ thi càng sát với đường tiệm cận. Hypebol nhận gốc toạ độ là tâm đối xứng và hai trục toạ độ là hai trục đối xứng.

Bằng cách này, em hãy cho biết bạn An đã vẽ được  hypebol (H) có phương trình như thế nào?

Elip có độ dài trục nhỏ là \(4\sqrt 6 \) và có một tiêu điểm F(5;0). Phương trình chính tắc của elip là:

Elip qua điểm \(M\left(2 ; \frac{5}{3}\right)\)và có một tiêu điểm F (-2;0) . Phương trình chính tắc của elip là: 

Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm  M(-2;2).

Đường elip \((E): \frac{x^{2}}{6}+\frac{y^{2}}{2}=1\) có tiêu cự bằng?

Trong mặt phẳng Oxy, cho điểm \(F\left( {0;\frac{1}{2}} \right)\),đường thẳng \(\Delta :{\rm{ }}y{\rm{ }} + \frac{1}{2} = 0\) và điểm M(x; y). Hệ thức giữa x và y là: