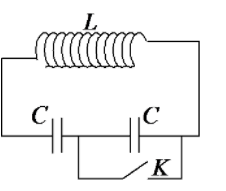
Mạch dao động kín, lí tưởng có L = 1 mH, C = 10 µF. Khi dao động cường độ dòng điện hiệu dụng I = 1 mA. Chọn gốc thời gian lúc điện tích bằng \(\frac{\sqrt{3}}{2}\) lần điện tích cực đại và tụ điện đang phóng điện. Viết biểu thức điện tích trên tụ điện.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTần số góc của mạch:\(\omega =\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{{{10}^{-3}}{{.10.10}^{-6}}}}={{10}^{4}}\text{ rad/s}\text{.}\)
Điện tích cực đại của tụ điện: \({{Q}_{0}}=\frac{{{I}_{0}}}{\omega }=\frac{\sqrt{2}{{.10}^{-3}}}{{{10}^{4}}}=\sqrt{2}{{.10}^{-7}}\text{ C}\text{.}\)
Biểu thức điện tích hai đầu tụ điện có dạng: \(q={{Q}_{0}}\cos \left( \omega t+\varphi \right)=\sqrt{2}{{.10}^{-7}}\cos \left( {{10}^{4}}t+\varphi \right)\text{ (V)}\text{.}\)
Tại thời điểm t = 0, ta có
\(q={{Q}_{0}}\cos \left( {{10}^{4}}.0+\varphi \right)=\frac{\sqrt{3}.{{Q}_{0}}}{2}\Rightarrow \cos \left( \varphi \right)=\frac{\sqrt{3}}{2}\Rightarrow \left[ \begin{align} & \varphi =\frac{\pi }{6}+k2\pi \\ & \varphi =-\frac{\pi }{6}+k2\pi \\ \end{align} \right..\)
Tại thời điểm t = 0, tụ điện phóng điện nên q giảm \(\Rightarrow \varphi =\frac{\pi }{6}+k2\pi =\frac{\pi }{6}.\) (k = 0)
Vậy biểu thức điện tích hai đầu tụ điện là \(\text{q}=\sqrt{2}.\text{1}{{\text{0}}^{-7}}\text{cos}\left( {{10}^{4}}t+\frac{\pi }{6} \right)\text{ }(\text{C}).\)
Câu hỏi liên quan
-
Một mạch dao động LC lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại của một bản tụ điện có độ lớn là 10-8 C và cường độ dòng điện cực đại qua cuộn cảm thuần là 62,8 mA. Tính tần số dao động điện từ tự do của mạch. Lấy \(\pi =3,14.\)
-
Mạch LC lí tưởng có tần số góc ω = 2.104 rad/s, L = 0,5 mH, hiệu điện thế cực đại trên hai bản tụ là 10 V. Điện tích cực đại của tụ điện là
-
Mạch dao động LC có L = 2 mH, C = 8 pF, Lấy p2 = 10. Thời gian từ lúc tụ bắt đầu phóng điện đến lúc có điện tích trên tụ bằng \(\frac{\sqrt{3}}{2}\) lần điện tích cực đại là
-
Để dao động điện từ của mạch dao động LC không bị tắt dần, người ta thường dùng biện pháp nào sau đây?
-
Mạch chọn sóng của một máy thu vô tuyến gồm một cuộn dây có độ tự cảm L và một bộ tụ điện gồm C0 mắc song song với một tụ C. Tụ C có điện dung thay đổi từ 10 nF đến 170 nF. Nhờ vậy mạch có thể thu được các sóng có bước sóng từ λ đến 3λ. Xác định C0.
-
Dòng điện trong mạch LC có biểu thức \(i=65\sin \left( 2500t+\frac{\pi }{3} \right)\text{ (mA)}\text{.}\) Tụ điện trong mạch có điện dung C = 750 nF. Độ tự cảm L của cuộn dây là
-
Trong một mạch dao động LC lý tưởng , L = 25 mH và C = 1,6 uF ở thời điểm t=0, cường độ mạch bằng 6,93mA, điện tích tụ điện bằng 0,8uC. Năng lượng của mạch dao động bằng
-
Chu kỳ dao động điện từ tự do trong mạch dao động LC được xác định bởi
-
Mạch dao động điện từ lí tưởng gồm cuộn dây thuần cảm và hai tụ điện giống hệt nhau ghép nối tiếp. Hai bản của một tụ được nối với nhau bằng khóa K. Ban đầu khóa K mở. Cung cấp năng lượng cho mạch dao động thì điện áp cực đại giữa hai đầu cuộn cảm là \(8\sqrt 6 V \) . Sau đó vào đúng thời điểm dòng điện qua cuộn dây có cường độ bằng giá trị hiệu dụng thì đóng khóa K. Hiệu điện thế cực đại giũa hai đầu cuộn dây sau khi đóng khóa K:
-
Mạch chọn sóng của máy thu vô tuyến gồm tụ điện C=2nF và cuộn cảm L=8,8μH. Để bắt được dải sóng ngắn (10m÷50m) cần ghép thêm một tụ xoay Cx có giá trị bằng bao nhiêu?
-
Xét mạch dao động tự dao LC, cuộn cảm có độ tự cảm L = 180 nH. Khi điện áp giữa hai bản tụ là u1 = 1,2 V thì cường độ dòng điện chạy qua cuộn cảm là i1 = 3 mA, còn khi điện áp giữa hai bản tụ là u2 = 0,9 V thì cường độ dòng điện chạy qua cuộn cảm là i2 = 4 mA. Điện dung của tụ điện bằng
-
Mạch dao động điện từ điều hoà gồm cuộn cảm L và tụ điện C, khi tăng điện dung của tụ điện lên 4 lần thì tần số dao động của mạch
-
Phát biểu nào sau đây là sai khi nói về năng lượng dao động điện từ tự do (dao động riêng) trong mạch dao động điện từ LC không điện trở thuần?
-
Chọn phương án sai khi nói về bổ sung năng lượng cho mạch:
-
Mạch dao động LC gồm cuộn cảm có độ tự cảm L = 2mH và tụ điện có điện dung C = 2pF, lấy π2 = 10. Tần số dao động của mạch là:
-
Công suất cần phải cung cấp thêm cho mạch để duy trì dao động có biểu thức:
-
Mạch dao động ở lối vào của một máy thu thanh gồm cuộc cảm thuần L và tụ điện có điện dung C1 đang thu được sóng điện từ có bước sóng 60 m. Biết rằng tần số dao động riêng của mạch dao động phải bằng tần số của sóng điện từ cần thu để có cộng hưởng. Nếu thay C1 bởi tụ điện có điện dung C2 thì mạch thu được sóng điện từ có bước sóng 80 m. Khi mắc bộ tụ điện( gồm C1 nối tiếp C2) với L thì mạch sẽ thu được sóng điện từ có bước sóng bằng
-
Mạch dao động lí tưởng LC được cung cấp một năng lượng từ một nguồn điện một chiều có suất điện động 8 V. Biết tần số góc của mạch dao động 4000 rad/s, điện tích cực đại của tụ là 10-6 C. Xác định độ tự cảm của cuộn dây
-
Mạch chọn sóng của máy thu vô tuyến gồm tụ điện C=2nF và cuộn cảm L=8,8μH. Mạch trên có thể bắt được sóng có bước sóng λ0 bằng bao nhiêu
-
Một con lắc đơn chiều dài l đang dao động điều hòa tại nơi có gia tốc rơi tự do g. Một mạch dao động gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C đang hoạt động. Biểu thức \(\frac{1}{{\sqrt {LC} }}\) có cùng đơn vị với biểu thức
