Mạch điện nối tiếp gồm điện trở thuần R, cuộn cảm thuần L và tụ điện C. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = U\sqrt 2 \cos \omega t\) (V), trong đó, \(\omega\) thay đổi được. Cho \(\omega\) từ 0 đến \(\infty \) thì điện áp hiệu dụng trên các phần tử đạt giá trị cực đại theo đúng thứ tự là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai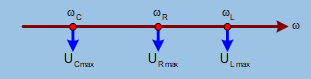
+ Khi \(\omega\) thay đổi thì: \(\left\{ \begin{array}{l} {U_{C\max }} \Leftrightarrow {Z_L} = {Z_\tau } \Leftrightarrow {\omega _C}L = \sqrt {\frac{L}{C} - \frac{{{R^2}}}{2}} < \sqrt {\frac{L}{C}} \Rightarrow {\omega _C} < \frac{1}{{\sqrt {LC} }}\\ {U_{L\max }}\left( {{P_{\max }};{I_{\max }}} \right) \Leftrightarrow Cong\,huong\, \Leftrightarrow {\omega _R} = \frac{1}{{\sqrt {LC} }}\\ {U_{L\max }} \Leftrightarrow {Z_C} = {Z_\tau } \Leftrightarrow \frac{1}{{{\omega _L}C}} = \sqrt {\frac{L}{C} - \frac{{{R^2}}}{2}} < \sqrt {\frac{L}{C}} \Rightarrow {\omega _L} > \frac{1}{{\sqrt {LC} }} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \omega _R^2 = {\omega _C}{\omega _L}\\ {\omega _C} < {\omega _R} < {\omega _L} \end{array} \right.\)











