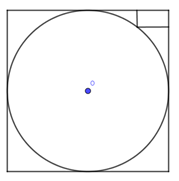
Một chiếc hộp hình trụ với bán kính đáy bằng chiều cao và bằng 10 cm. Một học sinh bỏ một miếng bìa hình vuông vào chiếc hộp đó và thấy hai cạnh đối diện của miếng bìa lần lượt là các dây cung của hai đường tròn đáy hộp và miếng bìa không song song với trục của hộp. Hỏi diện tích của miếng bìa đó bằng bao nhiêu?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiHộp hình trụ có R = h = 10. Gọi a là độ dài cạnh hình vuông (tấm bìa) đã cho. Gọi AB, CD lần lượt là cạnh hình vuông trên mặt đáy; cạnh trên mặt phía trên của hộp. Gọi E, F lần lượt là hình chiếu vuông góc của C, D xuống mặt đáy.
Ta có: \(\left\{ \begin{array}{l} EF = CD = AB\\ EF//CD//AB \end{array} \right.\)
⇒AEFB là hình chữ nhật nội tiếp đường tròn có bán kính R = 10.⇒ AEFB là hình chữ nhật nội tiếp đường tròn có bán kính R = 10.
Do đó
\( A{B^2} + B{F^2} = A{F^2} \Leftrightarrow A{B^2} + B{F^2} = 4{R^2} \Leftrightarrow {a^2} + B{F^2} = 4{R^2}\;\left( 1 \right)\)
Mặt khác theo pitago có:
\( B{D^2} = B{F^2} + F{D^2} \Leftrightarrow {a^2} = B{F^2} + {h^2}\;\left( 2 \right)\)
Từ (1) và (2) có:
\( 4{R^2} - {a^2} = {a^2} - {h^2} \Leftrightarrow {a^2} = \frac{{{h^2} + 4{R^2}}}{2} = \frac{{{{10}^2} + 4 \times {{10}^2}}}{2} = 250\)