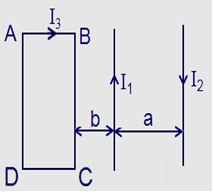
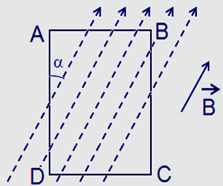
Một dây dẫn cứng có điện trở không đáng kể, được uốn thành khung phẳng ABCD nằm trong mặt phẳng nằm ngang, cạnh BA và CD đủ dài, song song nhau, cách nhau một khoảng l = 50 cm. Khung được đặt trong một từ trường đều có cảm ứng từ B = 0,5 T, đường sức từ hướng vuông góc với mặt phẳng của khung (như hình vẽ). Thanh kim loại MN có điện trở R = 0,5 W có thể trượt không ma sát dọc theo hai cạnh AB và CD. Thanh MN trượt đều với vận tốc v = 2 m/s dọc theo các thanh AB và CD. Thanh MN đang trượt đều thì ngừng tác dụng lực. Sau đó thanh còn có thể trượt thêm được đoạn đường bao nhiêu nếu khối lượng của thanh là m = 5 g
.PNG)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiKhi thanh MN chuyển động với vận tốc v thì dòng điện cảm ứng xuất hiện trên thanh theo chiều từ M đến N.
Suất điện động cảm ứng trong mạch: \(e_C=B.v.l\)
Cường độ dòng điện cảm ứng: \( I = \frac{{{e_C}}}{R} = \frac{{Bvl}}{R}\)
Lực từ tác dụng lên thanh MN hướng ngược chiều với \( \overrightarrow v \) và có độ lớn: \( {F_t} = BIl = \frac{{{B^2}{l^2}v}}{R}\)
Sau khi ngừng tác dụng lực, thanh chỉ còn chịu tác dụng của lực từ. Độ lớn trung bình của lực này là: \( \overline F = \frac{{{F_t}}}{2} = \frac{{{B^2}{l^2}v}}{{2R}}\)
Sau đó thanh này trượt thêm một đoạn đường s thì lực này thực hiện được một công: \( A = \overline F s = \frac{{{B^2}{l^2}v.s}}{{2R}}\)
Công này là công cản và đúng bằng độ biến thiên động năng của thanh nên:
\( - \frac{{{B^2}{l^2}v.s}}{{2R}} = 0 - \frac{1}{2}m{v^2} \to s = \frac{{mv}}{{{B^2}{I^2}}} = \frac{{0,005.2.0,5}}{{{{0,5}^2}{{.0,5}^2}}} = 0,08m\)
Câu hỏi liên quan
-
Một đoạn dây đồng CD chiều dài ℓ, có khối lượng m được treo ở hai đầu bằng sợi dây mềm, rất nhẹ, cách điện sao cho đoạn dây CD nằm ngang, tại nơi có gia tốc trọng trường g. Đưa đoạn dây đồng vào trong từ trường đều có cảm ứng từ B và các đường sức từ là những đường thẳng đứng hướng lên. Cho dòng điện qua dây CD có cường độ I sao cho BIℓ = 2mg thì dây treo lệch so với phương thẳng đứng một góc gần góc nào nhất sau đây?
-
Nhìn vào dạng đường sức từ, so sánh ống dây mang dòng điện với nam châm thẳng người ta thấy
-
Cảm ứng từ do dòng điện chạy qua ống dây dẫn hình trụ gây ra ở bên trong ống dây có độ lớn tăng lên khi
-
Một đoạn dây dẫn được đặt trong từ trường đều B = 0,5 T, l = 80 cm và B hợp với I một góc 300. Tìm I. Biết lực từ tác dụng lên đoạn dây là 0,06 N.
-
Một dây dẫn thẳng dài đặt trong không khí có dòng điện với cường độ chạy qua. Độ lớn cảmI ứng từ B do dòng điện này gây ra tại một điểm cách dây một đoạn được tính bởi công thức
-
Điều nào sau đây là không đúng? Cảm ứng từ tại mỗi điểm trong từ trường
-
Một khung dây có kích thước các cạnh là 20cm x 30cm đặt trong từ trường đều có B = 0,2 T. Cường độ dòng điện I = 2 A. Tính momen ngẫu lực từ cực đại tác dụng lên khung
-
Cho hai dây dẫn thẳng, dài, song song và một khung dây hình chữ nhật cùng nằm trong một mặt phẵng đặt trong không khí và có các dòng điện chạy qua như hình vẽ. Biết \(I_!=6A;_2=5A;I_3=4A;a=10cm'b=4cm;c=6cm;BC=20cm\). Xác định lực từ do từ trường của hai dòng điện chạy trong hai dây dẫn thẳng tác dụng lên cạnh BC của khung dây.
-
Cảm ứng từ do dòng điện chạy trong dây dẫn uốn thành vòng tròn gây ra tại tâm O của vòng dây có độ lớn giảm khi
-
Dây dẫn mang dòng điện không tương tác với
-
Cho hai dòng điện I1 = I2 = 6A chạy trong hai dây dẫn dài, song song, cách nhau 30cm theo cùng một chiều (hình vẽ). Xác định cảm ứng từ tổng hợp tại điểm M nằm trong mặt phẳng chứa hai dây dẫn, cách hai dây lần lượt MO1 = 10cm, MO2 = 20cm.
-
Hai thanh ray nằm ngang song song cách nhau 0,3cm đặt trong từ trường có cảm ứng từ vuông góc với mặt phẳng 2 thanh ray, hướng từ trên xuống. Một thanh kim loại đặt lên hai thanh ray. Cho dòng điện 50A chạy qua thanh kim loại đặt lên hai thanh ray. Biết hệ số ma sát giữa thanh kim loại và thanh ray là μ = 0,2 và khối lượng thanh kim loại là 0,5kg. Cảm ứng từ B có giá trị như thế nào để thanh kim loại có thể chuyển động?
-
Biết rằng cứ trong thời gian 10−3s thì cường độ dòng điện trong mạch giảm đều một lượng là 1 A và suất điện động tự cảm trong cuộn dây là 11,2 V. Độ tự cảm của cuộn dây bằng:
-
Một đoạn dây dẫn thẳng dài 89 cm được đặt vuông góc với các đường sức từ trong một từ trựờng đều. Cho biết khi dòng điện chạy qua đoạn dây dẫn có cường độ 23 A, thì đoạn dây dẫn này bị tác dụng một lực từ bằng 1,6N. Xác định cảm ứng từ của từ trường đều.
-
Độ lớn cảm ứng từ tại một điểm bên trong lòng ống dây có dòng điện đi qua sẽ tăng hay giảm bao nhiêu lần nếu số vòng dây và chiều dài ống dây đều tăng lên hai lần và cường độ dòng điện qua ống dây giảm bốn lần
-
Một dây dẫn mang dòng điện có chiều từ trái sang phải nằm trong một từ trường có chiều từ dưới lên thì lực từ có chiều
-
Nhận định nào sau đây không đúng về cảm ứng từ sinh bởi dòng điện chạy trong dây dẫn thẳng dài?
-
Hình vẽ nào dưới đây xác định sai hướng của véc tơ cảm ứng từ tại M gây bởi dòng điện thẳng dài vô hạn
-
Ống dây điện trên hình vẽ bị hút về phía thanh nam châm (Quan sát hình vẽ). Hãy chỉ rõ cực của thanh nam châm?
-
Hai dây dẫn thẳng, rất dài, đặt trong không khí, trùng với hai trục tọa độ vuông góc xOy. Dòng điện qua dây Ox chạy cùng chiều với chiều dương của trục tọa độ và có cường độ I1= 2A , dòng điện qua dây Oy chạy ngược chiều với chiều dương của trục tọa độ và có cường độ I2= 3 A. Xác định cảm ứng từ tổng hợp do hai dòng điện này gây ra tại điểm M có tọa độ x = 4 cm và y = -2 cm
