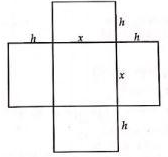
Một hộp không nắp được làm từ một mảnh các tông theo hình vẽ. Hộp có đáy là một hình vuông cạnh x(cm) , chiều cao là h (cm) và thể tích là 500cm3. Tìm độ dài cạnh hình vuông sao cho chiếc hộp làm ra tốn ít bìa các tông nhất.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiPhân tích: Ta có thể tích hộp được làm tính bằng công thức: \( V = x.x.h = {x^2}.h = 500\)
Khi đó lượng bìa các tông cần để làm hộp được tính bằng diện tích toàn phần của hộp:
\( {S_{tp}} = {S_{day}} + {S_{xq}} = x.x + 4hx = {x^2} + 4hx\)
Công việc của chúng ta bây giờ là đi tìm giá trị nhỏ nhất của Stp . Từ dữ kiện đã có ta có thể thay thế hx bằng \( \frac{{500}}{x}\)
Khi đó \(\begin{array}{l} {x^2} + 4\frac{{500}}{x} = {x^2} + \frac{{2000}}{x}\\ = {x^2} + \frac{{1000}}{x} + \frac{{1000}}{x} \ge 3\sqrt[3]{{{{1000}^2}}} \end{array}\)
(áp dụng bất đằng thức Cauchy)
Dấu bằng xảy ra khi và chỉ khi \( {x^2} = \frac{{1000}}{x} \Leftrightarrow {x^3} = 1000 \Leftrightarrow x = 10\)
Chú ý: Ngoài cách làm bằng bất đẳng thức như trên quý độc giả có thể làm bằng cách xét hàm số rồi đạo hàm tìm nghiệm phương trình f'(x)=0 cũng ra được kết quả.
Vậy đáp án đúng là: A.
.jpg.png)
.jpg.png)











