Một tấm kẽm hình vuông ABCD có cạnh bằng 30(cm). Người ta gập tấm kẽm theo hai cạnh EF và GH cho đến khi AD và BC trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết hai đáy.
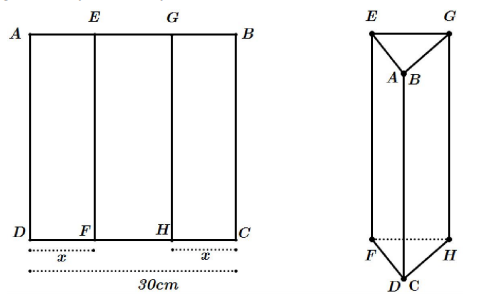
Giá trị của x để thể tích khối lăng trụ lớn nhất là
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có:\(D F=C H=x, F H=30-2 x \Rightarrow p_{\Delta D H F}=15\)
Thể tích khối lăng trụ như hình vẽ là
\(\begin{aligned} V=S_{F D H} \cdot E F &=30 \sqrt{15(15-x)(15-x)(15-30+2 x)} \\ &=30 \sqrt{15(15-x)^{2}(2 x-15)}, x \in\left(\frac{15}{2} ; 15\right) \end{aligned}\)
Xét hàm số \(f(x)=(15-x)^{2}(2 x-15)\)
\(\begin{array}{l} f^{\prime}(x)=-2(15-x)(2 x-15)+2(15-x)^{2}=-2(15-x)(3 x-30) \\ f^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l} x=10 \\ x=15 \end{array}\right. \end{array}\)
Bảng biến thiên:
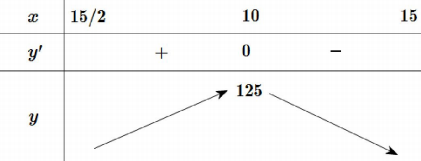
Dựa vào bảng biến thiên nhận thấy \(\max \limits_{\left(\frac{15}{2}, 15\right)} f(x)=125 \text { khi } x=10\)
Do đó thể tích khối lăng trụ như hình vẽ lớn nhất khi x =10(cm)
Khi đó \(V_{\max }=750 \sqrt{3}\left(\mathrm{cm}^{3}\right)\)
.png)