Cho hàm số \(y = {x^3} + 3{x^2} + mx + 1 - 2m.\).Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo sai\(y' = 3{x^2} + 6x + m\)
Hàm số đồng biến nếu y' ≥ 0. Ta có Δ' = 9 - 3m
TH1: m ≥ 3 ⇒ Δ' ≤ 0 .
Hàm số đồng biến trên R. Do đó m ≥ 3 không thỏa mãn yêu cầu đề bài
TH2: m < 3 ⇒ Δ' > 0 .
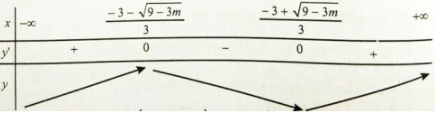
y’ có hai nghiệm phân biệt là \(x = \frac{{ - 3 \pm \sqrt {9 - 3m} }}{3}\)
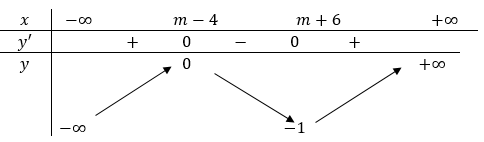
Từ bảng biến thiên, ta thấy không tồn tại m để hàm số đồng biến trên đoạn có độ dài bằng 1.
Từ TH1 và TH2, không tồn tại m thỏa mãn.
ADMICRO
YOMEDIA
ZUNIA9
.png)