Cho hàm số \(y = - {x^3} + 3{x^2} + 3mx - 1\), tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiTa có \(y' = - 3{x^2} + 6x + 3m\). Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình \( - 3{x^2} + 6x + 3m = 0\). Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 ⇒ m ≤ -1 khi đó, \( - 3{x^2} + 6x + 3m < 0\) nên hàm số nghịch biến trên R .
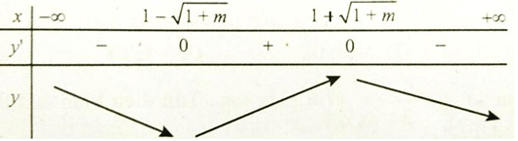
TH2: Δ' > 0 ⇒ m > -1; y' = 0 có hai nghiệm phân biệt là \(x = 1 \pm \sqrt {1 + m} \)
Hàm số nghịch biến trên (0; +∞) ⇔ 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1.
ADMICRO
YOMEDIA
ZUNIA9