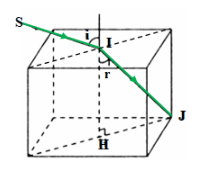
Một tia sáng được chiếu điến giữa của mặt trên của khối lập phương trong suốt, chiết suất n = 1,50 (hình vẽ). Tìm góc tới i lớn nhất để tia khúc xạ vào trong khối còn gặp mặt đáy của khối.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiGọi a là cạnh của khối lập phương. Áp dụng định luật khúc xạ ở mặt trên ta có: \(sini = n.sinr (1)\)
Điều kiện góc tới i=imax để tia khúc xạ vào trong khối còn gặp mặt đáp của khối là tia khúc xạ trùng với phương IJ với J là đỉnh của hình hộp như hình vẽ: r=rmax
Trong đó: \( IH = a;HJ = \frac{{a\sqrt 2 }}{2}\)
\( \to IJ = \sqrt {I{H^2} + H{J^2}} = \sqrt {{a^2} + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = a\sqrt {\frac{3}{2}} \)
+ Do đó: \( \sin {r_{\max }} = \frac{{HI}}{{IJ}} = \frac{{\frac{a}{{\sqrt 2 }}}}{{a\sqrt {\frac{3}{2}} }} = \frac{1}{{\sqrt 3 }}(2)\)
Từ (1) và (2) suy ra: \( \sin {i_{\max }} = 1,5.\frac{1}{{\sqrt 3 }} = \frac{{\sqrt 3 }}{2} \to {i_{\max }} = {60^0}\)
Câu hỏi liên quan
-
Tốc độ ánh sáng trong không khí là v1, trong nước là v2. Một tia sáng chiếu từ nước ra ngoài không khí với góc tới là i, có góc khúc xạ là r. Kết luận nào dưới đây là đúng?
-
Phát biểu nào sau đây là đúng?
-
Một người ngồi trên bờ hồ nhúng chân vào nước trong suốt. Biết chiết suất của nước là n=4/3. Khoảng cách thực từ bàn chân người đó đến mặt nước là 36 cm. Hỏi mắt người đó cảm thấy bàn chân cách mặt nước bao nhiêu?
-
Trong hiện tượng khúc xạ, góc khúc xạ
-
Một tia sáng chiếu xiên góc từ một môi trường sang môi trường chiết quang kém hơn với góc tới i thì tia khúc xạ hợp với pháp tuyến một góc khúc xạ r. Khi tăng góc tới i (với sini < n2/n1) thì góc khúc xạ r
-
Trong trường hợp nào sau đây, tia sáng không truyền thẳng khi
-
Một cái máng nước sâu 30 cm rộng 40 cm có hai thành bên thẳng đứng. Lúc máng cạn nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào máng đến một độ cao h thì bóng của thành A ngắn bớt đi 7 cm so với trước. Biết chiết suất của nước là n = 4/3. h = ?
-
Một bể chứa có thành cao 80cm và đáy phẳng dài 120cm. Biết độ cao mực nước trong bể là 60cm, chiết suất của nước là 4/3. Ánh nắng chiếu theo phương nghiêng góc 300 so với phương ngang thì độ dài bóng của thành bể tạo được ở đáy bể là
-
Hoàn thành câu phát biểu sau: “ Hiện tượng khúc xạ ánh sáng là hiện tượng tia sáng khi truyền từ môi trường trong suốt này sang môi trường trong suốt khác, tia sáng bị …… tại mặt phân cách giữa hai môi trường”
-
Một tia sáng đi từ chân không đén mặt chất lỏng có chiết suất là 4/3 dưới góc tới bằng 53o. Góc hợp bởi tia phản xạ và tia khúc xạ bằng
-
Một quả cầu trong suốt có bán kính 14 cm, chiết suất n. Tia tới SA song song song và cách đường kính MN của quả cầu đoạn 7 cm cho tia khúc xạ AN như hình. Chiết suất của quả cầu là?
.PNG)
-
Chọn câu sai.
-
Theo định luật khúc xạ thì
-
Chọn câu đúng nhất.
Khi tia sáng đi từ môi trường trong suốt n1 tới mặt phân cách với môi trường trong suốt n2 (với n2 > n1), tia sáng không vuông góc với mặt phân cách thì
-
Khi có khúc xạ liên tiếp qua nhiều môi trường có các mặt phân cách song song với nhau thì biểu thức nsini (với i là góc tới ở vùng có chiết suất n) thuộc về các môi trường
-
Một cây gậy cắm thẳng đứng xuống đáy hồ sâu 1,5 m. Phần gậy nhô lên khỏi mặt nước là 0,5 m. Ánh sáng mặt trời chiếu xuống hồ theo phương hợp với pháp tuyến mặt nước góc 60° Tính chiều dài bóng cây gậy trên mặt nước và dưới đáy hồ?
-
Một tấm thuỷ tinh có hai mặt giới hạn là hai mặt phẳng song song với nhau (gọi là bản mặt song song), bề dày của nó là 10cm, chiết suất là 1,5 được đặt trong không khí. Chiếu tới một mặt của bản mặt song song một tia sáng có góc tới bằng 450, khi đó tia ló khỏi bản sẽ đi ra mặt còn lại. Phương của tia ló có đặc điểm nào sau đây ?
-
Chiếu một tia sáng đơn sắc đi từ không khí vào môi trường có chiết suất n với góc tới i. Tia phản xạ vuông góc với tia khúc xạ. Hệ thức nào sau đây là đúng?
-
Hiện tượng khúc xạ là hiện tượng
-
Chiếu một tia sáng đơn sắc đi từ không khí vào môi trường có chiết suất n, sao cho tia phản xạ vuông góc với tia khúc xạ. Khi đó góc tới i được tính theo công thức
