Một vật dao động theo phương trình \( x = 20\cos \left( {\frac{{5\pi }}{3}t - \frac{\pi }{6}} \right){\mkern 1mu} {\mkern 1mu} cm\). Kể từ lúc t = 0 đến lúc vật đi qua vị trí x = - 10 cm theo chiều âm lần thứ 2015 thì lực hồi phục sinh công dương trong thời gian
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiChu kì của dao động: \( T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{{5\pi }}{3}}} = 1,2{\mkern 1mu} {\mkern 1mu} \left( s \right)\)
Nhận xét: lực hồi phục sinh công dương, nên công suất của lực hồi phục P=Fph.v>0→ lực hồi phục và vận tốc cùng dấu, khi vật hướng về VTCB. → Trong 1 chu kì, lực hồi phục sinh công dương trong thời gian T2
Pha ban đầu của dao động: \( \varphi = - \frac{\pi }{6}{\mkern 1mu} {\mkern 1mu} \left( {rad} \right)\)
Trong 1 chu kì, vật qua vị trí x = - 10 cm theo chiều âm 1 lần.
Ta có: 2015 = 2014 + 1
Thời gian lực phục hồi sinh công dương từ lúc t = 0 đến lúc vật đi qua vị trí x = - 10 cm theo chiều âm lần thứ 2015 là \( 2014.\frac{T}{2}\) và thời gian lực phục hồi sinh công dương từ lúc t = 0 đến lúc vật qua vị trí x = - 10 cm theo chiều âm lần đầu tiên.
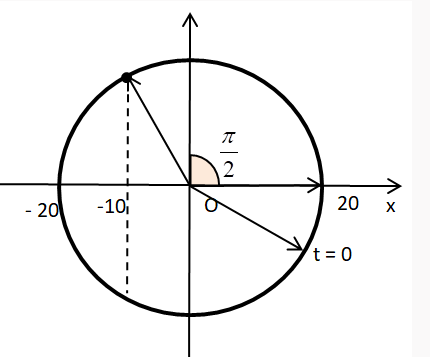
Ta có vòng tròn lượng giác:
Từ VTLG, ta thấy từ lúc t = 0 đến lúc vật qua vị trí x = - 10 cm theo chiều âm lần đầu tiên, lực hồi phục sinh công dương ứng với thời gian vật đi từ vị trí biên dương đến VTCB:
\(t= \frac{{{\rm{\Delta }}\varphi }}{\omega } = \frac{{{\rm{\Delta }}\varphi }}{{\frac{{2\pi }}{T}}} = \frac{{\frac{\pi }{2}}}{{\frac{{2\pi }}{T}}} = \frac{T}{4}\)
Vậy thời gian cần tìm là:
\(2014.\frac{T}{2} + \frac{T}{4} = \frac{{4029}}{4}T = \frac{{4029}}{4}.1,2 = 1208,7{\mkern 1mu} {\mkern 1mu} \left( s \right)\)
Chọn B.