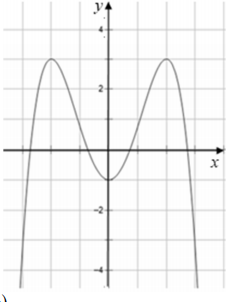
Qua điểm A( 0;2 ) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x4-2x2+2?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiGọi d là tiếp tuyến của đồ thị hàm số đã cho.
Vì A ∈ d nên phương trình của d có dạng: y = kx+2
Vì d tiếp xúc với đồ thị (C) nên hệ
\(\left\{ \begin{array}{l}
{x^4} - 2{x^2} + 2 = kx + 2\,\,\left( 1 \right)\\
4{x^3} - 4x = k\,\,\left( 2 \right)
\end{array} \right.\) có nghiệm
Thay (2) vào (1) ta suy ra được \(\left[ \begin{array}{l}
x = 0\\
x = \pm \sqrt {\frac{2}{3}}
\end{array} \right.\)
Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
ADMICRO
YOMEDIA
ZUNIA9
.png)
.png)