Tìm giá trị nhỏ nhất của hàm số \(f(x)=\sqrt{x+\frac{1}{x}}\) trên khoảng \((0 ;+\infty)\)?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiHàm số đã cho xác định và liên tục trên khoảng \((0 ;+\infty)\)
\(f^{\prime}(x)=\frac{\left(x+\frac{1}{x}\right)^{\prime}}{2 \sqrt{x+\frac{1}{x}}}=\frac{1-\frac{1}{x^{2}}}{2 \sqrt{x+\frac{1}{x}}}=0 \Leftrightarrow x^{2}=1 \Leftrightarrow\left[\begin{array}{l} x=1 \in(0 ;+\infty) \\ x=-1 \notin(0 ;+\infty) \end{array}\right.\)
Bảng biến thiên
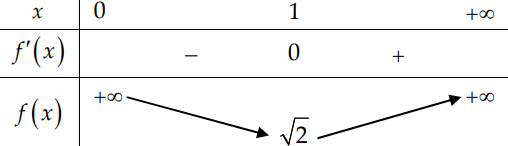
Vậy \(\min\limits _{(0 ;+\infty)} f(x)=\sqrt{2}\)
ADMICRO
YOMEDIA
ZUNIA9
.jpg.png)











