Tìm tất cả các giá trị của m để hàm số \(f(x)=\left|x^{3}+3 x^{2}-3+m\right|\) có ba điểm cực trị.
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
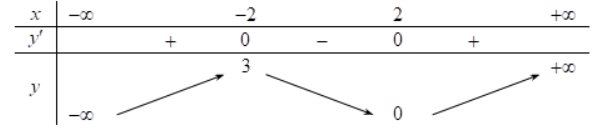
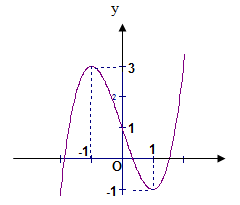
Báo saiXét hàm số \(y=g(x)=x^{3}+3 x^{2}-3+m \text { trên } \mathbb{R}\) . Hệ số a= 1> 0.
Hàm số có \(y^{\prime}=g^{\prime}(x)=3 x^{2}+6 x ; y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} x=0 \\ x=-2 \end{array}\right.\) . Hàm số y=g(x) luôn có hai cực trị.
Nếu g (x)=0 có 3 nghiệm hay trục hoành giao với đồ thị hàm số tại ba điểm phân biệt thì hàm số \(y=|g(x)|\) có năm cực trị.
Nếu g(x)=0 có một hoặc hai nghiệm thì hàm số \(y=|g(x)|\) sẽ có ba cực trị.
Điều kiện: \(g\left(x_{c d}\right) \cdot g\left(x_{c t}\right) \geq 0 \Leftrightarrow g(0) \cdot g(-2) \geq 0 \text { hay }(-3+m)(1+m) \geq 0 \Leftrightarrow\left[\begin{array}{l} m \geq 3 \\ m \leq-1 \end{array}\right.\)
.png)
.png)