Tìm tất cả các giá trị của tham số m để hàm số \(y=\frac{1}{m \log _{3}^{2} x-4 \log _{3} x+m+3}\) xác định trên khoảng \((0 ;+\infty)\)
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiĐiều kiện: x >0 . Hàm số xác định khi
\(m \log _{3}^{2} x-4 \log _{3} x+m+3 \neq 0 \Leftrightarrow m\left(\log _{3}^{2} x+1\right) \neq 4 \log _{3} x-3 \Leftrightarrow m \neq \frac{4 \log _{3} x-3}{\log _{3}^{2} x+1}, \forall x \in(0 ;+\infty) .\)
\(\text { Để hàm số xác định trên }(0 ;+\infty) \text { thì phương trình } m=\frac{4 \log _{3} x-3}{\log _{3}^{2} x+1} \text { vô nghiệm } \forall x \in(0 ;+\infty)\)
\(\text { Xét hàm số } y=\frac{4 \log _{3} x-3}{\log _{2}^{2} x+1} \text { . }\)
\(\text { Đặt } \log _{3} x=t \text { khi đó ta có } y=\frac{4 t-3}{t^{2}+1}, y^{\prime}=\frac{-4 t^{2}+6 t+4}{\left(t^{2}+1\right)^{2}} \Rightarrow y^{\prime}=0 \Leftrightarrow\left[\begin{array}{l} t=\frac{-1}{2} \\ t=2 \end{array}\right. \text { . }\)
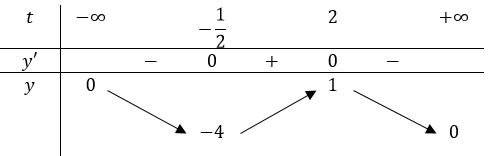
Bảng biến thiên
Vậy để \(\text { hàm số xác định trên }(0 ;+\infty) \text { thì } m \in(-\infty ;-4) \cup(1 ;+\infty) \text { . }\)