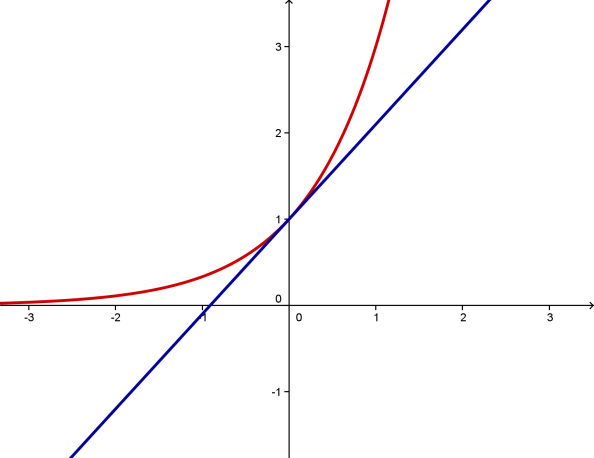
Tìm tất cả các giá trị thực của tham số m để phương trình \({{3}^{x}}=mx+1\) có hai nghiệm phân biệt?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo saiTa có: Số nghiệm của phương trình \({{3}^{x}}=mx+1\) phụ thuộc vào số giao điểm của đồ thị hàm số \(y={{3}^{x}}\) và đường thẳng \(y=mx+1\).
Ta thấy \(y=mx+1\) luôn đi qua điểm cố định \(\left( 0;\,\,1 \right)\) nên
+Nếu m=0: phương trình có nghiệm duy nhất
+ Nếu m<0 :\(y=mx+1\) là hàm nghịch biến nên có đồ thị cắt đồ thị hàm số \(y={{3}^{x}}\) tại một điểm duy nhất.
+ Nếu m>0: Để thỏa mãn ycbt thì đường thẳng\(y=mx+1\) phải khác tiếp tuyến của đồ thị hàm số \(y={{3}^{x}}\) tại điểm \(\left( 0;\,\,1 \right)\), tức là \(m\ne \ln 3\).
Vậy \(\left\{ \begin{array}{l} m > 0\\ m \ne \ln 3 \end{array} \right.\)