Tìm tất cả các giá trị thực của tham số m để phương trình \((\sqrt{3}-\sqrt{2})^{x}+(\sqrt{3}+\sqrt{2})^{x}-2 m=0\) có nghiệm.
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
Báo saiĐặt \(t=(\sqrt{3}+\sqrt{2})^{x}>0\) thì phương trình trở thành :
\(\frac{1}{t}+t-2 m=0 \Leftrightarrow 2 m=t+\frac{1}{t}\)
Xét \(f(t)=t+\frac{1}{t} \Rightarrow f^{\prime}(t)=1-\frac{1}{t^{2}}=0\)
\(f^{\prime}(t)=0 \Leftrightarrow t=1(\text { do } t>0)\)
BBT:
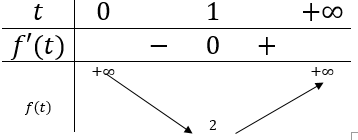
Phương trình có nghiệm \(\Leftrightarrow 2 m \geq 2 \Leftrightarrow m \geq 1\)
ADMICRO
YOMEDIA
ZUNIA9











