Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình \(\sqrt {\left( {1 + 2x} \right)\left( {3 - m} \right)} \; > \;m + 2{x^2} - 5x - 3\) nghiệm đúng với mọi \(x \in \left[ {\begin{array}{*{20}{c}}
{\frac{{ - 1}}{2};}3
\end{array}} \right]\)?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Lời giải:
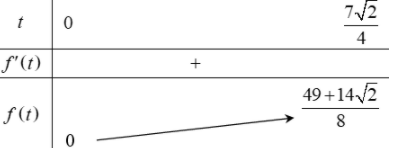
Báo saiĐặt \(t = \sqrt {\left( {1 + 2x} \right)\left( {3 - x} \right)} \)
Khi \(x \in \left[ {\begin{array}{*{20}{c}}
{\frac{{ - 1}}{2};}3
\end{array}} \right] \Rightarrow t \in \left[ {0;\frac{{7\sqrt 2 }}{4}} \right]\)
Thay vào bpt ta được:
\(f\left( t \right) = {t^2} + t > m\)
BBT
Từ BBT ta có m < 0.
ADMICRO
YOMEDIA
ZUNIA9