(1) Hàm số \(y = \sin x\) và \(y = \cos x\) cùng đồng biến trên khoảng \(\left( {\dfrac{{3\pi }}{2};2\pi } \right)\).
(2) Đồ thị hàm số \(y = 2019\sin x + 10\cos x\) cắt trục hoành tại vô số điểm.
(3) Đồ thị hàm số \(y = \tan x\) và \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) chỉ có một điểm chung.
(4) Với \( \in \left( {\pi ;\dfrac{{3\pi }}{2}} \right)\) các hàm số \(y = \tan \left( {\pi - x} \right)\), \(y = \cot \left( {\pi - x} \right)\), \(y = \sin \left( {\pi - x} \right)\) đều nhận giá trị âm.
Trong các mệnh đề trên, số mệnh đề sai là:
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
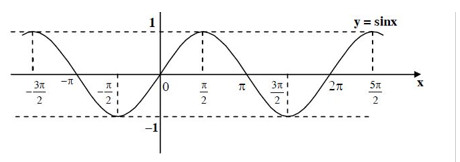
Báo saiXét mệnh đề (1): Ta có đồ thị hàm số \(y = \sin x\) và \(y = \cos x\) như sau:
Đồ thị hàm số \(y = \sin x\):
Đồ thị hàm số \(y = \cos x\):
.jpg)
Hai hàm số này cùng đồng biến trên \(\left( {\dfrac{{3\pi }}{2};2\pi } \right)\). Do đó mệnh đề (1) đúng.
Xét mệnh đề (2): Phương trình hoành độ giao điểm: \(2019\sin x + 10\cos x = 0\) \( \Leftrightarrow \tan x = - \dfrac{{10}}{{2019}}\).
Do đó phương trình này có vô số nghiệm, nên mệnh đề (2) đúng.
Xét mệnh đề (3): Phương trình hoành độ giao điểm:
\(\tan x = \cot x \Leftrightarrow \tan x = \dfrac{1}{{\tan x}}\)\( \Leftrightarrow \left[ \begin{array}{l}\tan x = 1\\\tan x = - 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{4} + k\pi \\x = - \dfrac{\pi }{4} + k\pi \end{array} \right.\,\,\left( {k \in \mathbb{Z}} \right)\).
+ Xét họ nghiệm \(x = \dfrac{\pi }{4} + k\pi \).
\(0 < \dfrac{\pi }{4} + k\pi < \pi \Leftrightarrow - \dfrac{1}{4} < k < \dfrac{3}{4},\,\,k \in \mathbb{Z}\) \( \Rightarrow k = 0 \Rightarrow x = \dfrac{\pi }{4}\).
+ Xét họ nghiệm \(x = - \dfrac{\pi }{4} + k\pi \).
\(0 < - \dfrac{\pi }{4} + k\pi < \pi \Leftrightarrow \dfrac{1}{4} < k < \dfrac{5}{4},\,\,k \in \mathbb{Z}\) \( \Rightarrow k = 1 \Rightarrow x = \dfrac{{3\pi }}{4}\).
Vậy đồ thị hàm số \(y = \tan x\) và \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) có 2 điểm chung, do đó mệnh đề (3) sai.
Xét mệnh đề (4):
Ta có: \(\tan \left( {\pi - x} \right) = - \tan x,\,\,\cot \left( {\pi - x} \right) = - \cot x,\,\,\sin \left( {\pi - x} \right) = \sin x\).
Trên khoảng \(\left( {\pi ;\dfrac{{3\pi }}{2}} \right)\) ta có: \(\left\{ \begin{array}{l}\tan x > 0 \Leftrightarrow - \tan x < 0\\\cot x > 0 \Leftrightarrow - \cot x < 0\\\sin x < 0\end{array} \right.\).
Do đó mệnh đề (4) đúng.
Vậy có 1 mệnh đề sai.
Chọn D.
Đề thi giữa HK1 môn Toán 11 năm 2022-2023
Trường THPT Trần Phú











