Cho 2 đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\angle xOy = \dfrac{2}{3}\angle xOy'\). Tính số đo \(\angle xOy'\)?
Chính xác
Xem lời giải
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
ATNETWORK
Chủ đề: Đề thi Học Kỳ/Giữa Kỳ
Môn: Toán Lớp 7
Lời giải:
Báo sai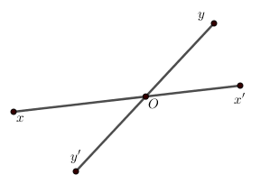
Vì \(\angle xOy\) và \(\angle x'Oy\) là hai góc kề bù nên \(\angle xOy + \angle x'Oy = {180^0}\)
Mà \(\angle xOy = \dfrac{2}{3}\angle x'Oy\)
Suy ra \(\dfrac{2}{3}\angle x'Oy + \angle xOy' = {180^0}\)
\(\dfrac{5}{3}\angle xOy' = {180^0}\)
\(\begin{array}{l}\angle xOy' = {180^0}:\dfrac{5}{3} = {180^0}.\dfrac{3}{5}\\\angle xOy' = {108^0}\end{array}\)
Vậy \(\angle xOy' = {108^0}\)
Chọn C.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
Đề thi giữa HK1 môn Toán 7 năm 2023-2024
Trường THCS Ngô Sĩ Liên
08/01/2025
48 lượt thi
0/40
Bắt đầu thi
ADMICRO
YOMEDIA
ZUNIA9