Trong mp tọa độ Oxy, cho đường tròn lượng giác. M thuộc đường tròn sao cho \(\widehat{AOM}=\frac{\pi }{6}\) (M thuộc góc phần tư thứ tư). Số đo \(\overset{\curvearrowright }{\mathop{AM}}\,\) có thể là giá trị nào?
Suy nghĩ và trả lời câu hỏi trước khi xem đáp án
Lời giải:
Báo sai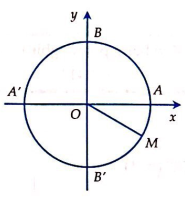
Vì M thuộc góc phần tư thứ IV và \(\widehat{AOM}=30{}^\circ \) nên đây là góc tính theo chiều âm
\(\Rightarrow \widehat{AOM}=\alpha \) theo chiều dương là \(\alpha =2\pi -\frac{\pi }{6}+k2\pi \left( k\in \mathbb{Z} \right)\)
\(\alpha =\frac{11\pi }{6}+k2\pi \left( k\in \mathbb{Z} \right)\)
\(\Rightarrow \) sđ \(\overset{\curvearrowright }{\mathop{AM}}\,=\frac{11\pi }{6}+k2\pi \left( k\in \mathbb{Z} \right)\)
Vì \(k\in \mathbb{Z}\) nên chỉ có đáp án C thỏa mãn (với \(k=-2\)).
Đáp án C.
Đề thi giữa HK1 môn Toán 11 CTST năm 2023-2024
Trường THPT Trưng Vương