Đề thi giữa HK1 môn Toán 11 CTST năm 2023-2024
Trường THPT Trưng Vương
-
Câu 1:
Trong mp tọa độ Oxy, cho đường tròn lượng giác. M thuộc đường tròn sao cho \(\widehat{AOM}=\frac{\pi }{6}\) (M thuộc góc phần tư thứ tư). Số đo \(\overset{\curvearrowright }{\mathop{AM}}\,\) có thể là giá trị nào?
A. \(\frac{5\pi }{6}\)
B. \(\frac{\pi }{6}\)
C. \(\frac{-13\pi }{6}\)
D. \(\frac{-11\pi }{6}\)
-
Câu 2:
Đổi số đo cung \(\frac{5}{6}\text{rad}\) sang độ, phút, giây ta được?
A. \(47{}^\circ 44'47''\)
B. \(37{}^\circ 33'37''\)
C. \(150{}^\circ \)
D. \(30{}^\circ \)
-
Câu 3:
Chọn điểm \(A\left( 1;0 \right)\) làm điểm đầu cung lượng giác trên đường tròn lượng giác. Tìm điểm cuối M của cung lượng giác có số đo \(\frac{27\pi }{4}\)?
A. M là điểm chính giữa của cung phần tư thứ nhất
B. M là điểm chính giữa của cung phần tư thứ hai
C. M là điểm chính giữa của cung phần tư thứ ba
D. M là điểm chính giữa của cung phần tư thứ tư
-
Câu 4:
Cho 4 cung (trên một đường tròn định hướng): \(\alpha =\frac{\pi }{3};\beta =\frac{10\pi }{3}\); \(\gamma =\frac{-5\pi }{3};\delta =\frac{-7\pi }{3}\). Các cung có điểm cuối cùng trùng nhau là?
A. \(\alpha \) và \(\delta \)
B. \(\alpha \) và \(\beta \)
C. \(\beta \) và \(\delta \)
D. \(\alpha \) và \(\gamma \)
-
Câu 5:
Cho ĐT \(\left( O;R \right)\) ngoại tiếp lục giác đều ABCDEF. Khi đó số đo cung của đường tròn có độ dài bằng chu vi lục giác theo độ và rad lần lượt là?
A. \(360{}^\circ \) và \(2\pi \)
B. \(360{}^\circ \) và \(\pi \)
C. \(\frac{1080{}^\circ }{\pi }\) và 6
D. \(1080{}^\circ \) và \(6\pi \)
-
Câu 6:
Giá trị của biểu thức \(P=\sin x\) với \(x=420{}^\circ \) có kết quả là?
A. \(\frac{\sqrt{3}}{2}\)
B. \(-\frac{\sqrt{3}}{2}\)
C. \(\frac{1}{2}\)
D. \(-\frac{1}{2}\)
-
Câu 7:
Cho \(\sin \alpha =\frac{-4}{5}\) và \(\pi <\alpha <\frac{3\pi }{2}\). Giá trị của \(\cos \alpha \) là?
A. \(\frac{3}{5}\)
B. \(\frac{-3}{5}\)
C. \(\pm \frac{3}{5}\)
D. \(\frac{9}{25}\)
-
Câu 8:
Trên đường tròn lượng giác, cho cung \(\overset\frown{AM}\) có sđ \(\overset\frown{AM}=\alpha \), sin của góc α là?
A. tỉ số \(\frac{\sin \alpha }{\cos \alpha }\)
B. tỉ số \(\frac{\cos \alpha }{\sin \alpha }\)
C. Tung độ y của M
D. Hoành độ x của M
-
Câu 9:
Giá trị của biểu thức \(P=\sin x+x\) với \(x=390{}^\circ \) là?
A. 389,5
B. \(\frac{13\pi }{6}+\frac{1}{2}\)
C. \(390,5\)
D. \(\frac{13\pi }{6}-\frac{1}{2}\)
-
Câu 10:
Hệ thức liên hệ giữa hai cung bù nhau (\(\alpha \) và \(\pi -\alpha \)) nào dưới đây sai?
A. \(\tan \left( \pi -\alpha \right)=-\tan \alpha \)
B. \(\sin \left( \pi -a \right)=-\sin \alpha \)
C. \(\cos \left( \pi -\alpha \right)=-\cos \alpha \)
D. \(\cot \left( \pi -\alpha \right)=-\cot \alpha \)
-
Câu 11:
Công thức nhân đôi nào sau đây là đúng?
A. \(\sin 2a=\sin a\cos a\)
B. \(\cos 2a={{\cos }^{2}}a-{{\sin }^{2}}a=2{{\cos }^{2}}a-1=1+2{{\sin }^{2}}a\)
C. \(\tan 2a=\frac{2\tan a}{1-{{\tan }^{2}}a}\)
D. \(\cot 2a=\frac{{{\cot }^{2}}a+1}{2\cot a}\)
-
Câu 12:
Cho \(\cos \alpha =\frac{1}{3}\). Khi đó giá trị biểu thức \(B=\sin \left( \alpha -\frac{\pi }{4} \right)-\cos \left( \alpha -\frac{\pi }{4} \right)\) là?
A. \(\frac{\sqrt{2}}{3}\)
B. \(\frac{-\sqrt{2}}{3}\)
C. \(\frac{2\sqrt{2}}{3}-\frac{1}{3}\)
D. \(\frac{-2\sqrt{2}}{3}-\frac{1}{3}\)
-
Câu 13:
Cho \(\sin \alpha =\frac{-5}{13};\pi \le \alpha \le \frac{3\pi }{2}\). Gía trị biểu thức \(\sin 2\alpha \cos 2\alpha +\tan 2\alpha \) gần nhất với giá trị nào?
A. \(-2\)
B. \(-1\)
C. 1
D. 2
-
Câu 14:
Công thức biến đổi tích thành tổng nào dưới đây đúng?
A. \(\sin a\cos b=\frac{1}{2}\left[ \sin \left( a-b \right)+\sin \left( a+b \right) \right]\)
B. \(\sin a\sin b=\frac{1}{2}\left[ \cos \left( a-b \right)-\cos \left( a+b \right) \right]\)
C. \(\cos a\cos b=\frac{1}{2}\left[ \cos \left( a-b \right)+\cos \left( a+b \right) \right]\)
D. Tất cả đều đúng.
-
Câu 15:
Cho \(\cot \frac{\pi }{14}=a\). Giá trị biểu thức \(K=\sin \frac{2\pi }{7}+\sin \frac{4\pi }{7}+\sin \frac{6\pi }{7}\) bằng?
A. \(a\)
B. \(\frac{a}{2}\)
C. \(\frac{4a\left( {{a}^{2}}-1 \right)\left( 3{{a}^{2}}-1 \right)}{{{\left( {{a}^{2}}+1 \right)}^{3}}}\)
D. \(\frac{{{\left( {{a}^{2}}+1 \right)}^{3}}}{4a\left( {{a}^{2}}-1 \right)\left( 3{{a}^{2}}-1 \right)}\)
-
Câu 16:
Hàm số y=sinx xác định trên khoảng nào?
A. R\kπ,k∈Z
B. R∖{kπ2,k∈Z}
C. R∖{π2+kπ,k∈Z}
D. \(R\)
-
Câu 17:
Hàm số nào dưới đây có đồ thị không là đường hình sin?
A. y = sinx
B. y = cotx
C. y = cosx
D. y = sin2x
-
Câu 18:
Đường cong trong hình có thể là đồ thị của hàm số nào dưới đây?
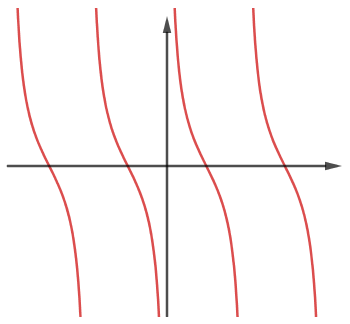
A. y = cotx
B. y = tanx
C. y = sinx
D. y = cosx
-
Câu 19:
Đồ thị hàm số y = tanx đi qua điểm nào dưới đây?
A. O(0;0)
B. M(0;1)
C. N(π/2;0)
D. P(1;0)
-
Câu 20:
Hàm số y = cosx nghịch biến trên mỗi khoảng?
A. (π/2 + k2π; 3π/2 + k2π)
B. (−π + k2π; k2π)
C. (k2π; π + k2π)
D. 0
-
Câu 21:
Nghiệm \(x = \dfrac{{2\pi }}{3}\) là của phương trình nào dưới đây?
A. \(\sin x = - \dfrac{1}{2}\)
B. \(\cot x = - \dfrac{{\sqrt 3 }}{3}\)
C. \(\tan x = \sqrt 3 \)
D. \(\cos x = - \dfrac{1}{2}\)
-
Câu 22:
Phương trình \({\tan ^2}x = 3\) có nghiệm là?
A. \(x = \pm \dfrac{\pi }{3} + k\pi \)
B. \(x = - \dfrac{\pi }{6} + k\pi \)
C. Vô nghiệm
D. \(x = \dfrac{\pi }{6} + k\pi \)
-
Câu 23:
Tìm nghiệm của phương trình \(\cot \left( {x - \dfrac{\pi }{3}} \right) = \dfrac{{\sqrt 3 }}{3}\)?
A. \(x = \dfrac{\pi }{3} + k\pi ,k \in Z\).
B. \(x = \dfrac{\pi }{2} + k2\pi ,k \in Z\).
C. \(x = \dfrac{{2\pi }}{3} + k\pi ,k \in Z\).
D. \(x = k\pi ,k \in Z\).
-
Câu 24:
Nghiệm của phương trình \(\tan \dfrac{x}{2} = \dfrac{{\sqrt 3 }}{3}\) là?
A. \(x = \dfrac{\pi }{3} + k3\pi \)
B. \(x = \dfrac{\pi }{3} + k4\pi \)
C. \(x = \dfrac{\pi }{3} + k2\pi \)
D. \(x = \dfrac{\pi }{3} + k\pi \)
-
Câu 25:
Giải phương trình lượng giác sau: \(\cot x = \cot 2x\)?
A. \(x = \frac{{k\pi }}{2}\,\,\left( {k \in Z} \right)\)
B. \(x = k\pi \,\,\left( {k \in Z} \right)\)
C. \(x = k2\pi \,\,\left( {k \in Z} \right)\)
D. Kết quả khác
-
Câu 26:
Phát biểu nào dưới đây đúng?
A. Tồn tại một mặt bên của hình chóp không là tam giác.
B. Hình chóp có tất cả các mặt là hình tam giác.
C. Số cạnh bên của hình chóp bằng số mặt của nó.
D. Tất cả mặt bên của hình chóp là hình tam giác.
-
Câu 27:
Trong không gian cho tứ diện \(ABCD\). Gọi \(M\,,\,\,N\) lần lượt là trung điểm của \(AB\,,\,\,CD\), \(G\) là trọng tâm tam giác \(BCD\). Đường thẳng \(AG\) cắt đường thẳng nào?
A. Đường thẳng \(MN\).
B. Đường thẳng \(CD\).
C. Đường thẳng \(CM\).
D. Đường thẳng \(DN\).
-
Câu 28:
Trong các mệnh đề sau, mệnh đề nào dưới đây là sai?
A. Có duy nhất một mặt phẳng đi qua hai đường thẳng mà hai đường thẳng này lần lượt nằm trên hai mặt phẳng cắt nhau.
B. Có duy nhất một mặt phẳng đi qua hai đường thẳng cắt nhau cho trước.
C. Nếu hai mặt phẳng có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.
D. Ba điểm không thẳng hàng cùng thuộc một mặt phẳng duy nhất.
-
Câu 29:
Cho hình chóp \(S.ABCD\) đáy là hình bình hành tâm \(O\). Gọi \(M,N\)lần lượt là trung điểm của \(SA,SD\). Trong các mệnh đề sau, mệnh đề nào đúng?
A. \(\left( SMN \right)\text{//}\left( SBC \right)\).
B. \(\left( OMN \right)\text{//}\left( SBC \right)\).
C. \(\left( OMN \right)\text{//}\left( SAD \right)\).
D. \(\left( OMG \right)\text{//}\left( SCD \right)\).
-
Câu 30:
Cho tứ diện \(ABCD\). Gọi \(M\) là trung điểm của \(BC\), \(G,{G}'\) lần lượt là trọng tâm của \(\Delta ABC,\Delta BCD\). Tìm mệnh đề sai?
A. \(AD\text{//}\left( BG{G}' \right)\).
B. \(AD\text{//}G{G}'\).
C. \(G{G}'\text{//}\left( ACD \right)\).
D. \(BC\text{//}G{G}'\).
-
Câu 31:
Cho hai đường thẳng phân biệt \(a\) và \(b\) trong không gian. Có bao nhiêu vị trí tương đối giữa \(a\) và \(b\)?
A. 4
B. 3
C. 1
D. 2
-
Câu 32:
Cho hình chóp \(S.ABCD\) với đáy là tứ giác \(ABCD\) có các cạnh đối không song song. Giả sử \(AC\cap BD=O\), \(AD\cap BC=I\). Giao tuyến của hai mặt phẳng \(\left( SAC \right)\) và \(\left( SBD \right)\) là?
A. \(SC\).
B. \(SO\).
C. \(SI\).
D. \(SB\).
-
Câu 33:
Cho hình chóp \(S.ABCD,\) đáy \(ABCD\) là hình bình hành. Giao tuyến của hai mặt phẳng \(\left( SAD \right)\) và \(\left( SBC \right)\) là đường thẳng song song với đường thẳng nào sau đây?
A. AD
B. AC
C. DC
D. BD
-
Câu 34:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\)là hình bình hành. Gọi \(d\) là giao tuyến của hai mặt phẳng \(\left( SAD \right)\And \left( SBC \right)\). Khẳng định nào sau đây đúng?
A. \(d\) qua \(S\) và song song với \(CD\).
B. \(d\) qua \(S\) và song song với \(AB\).
C. \(d\) qua \(S\) và song song với \(BC\).
D. \(d\) qua \(S\) và song song với \(BD\).
-
Câu 35:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, \(AB\text{//}CD\). Gọi \(M\),\)N\), \(Q\) lần lượt là trung điểm của \(BC\), \(AD\) và \(SB\). Giao tuyến của hai mp \(\left( SAB \right)\) và \(\left( MNQ \right)\)?
A. Đường thẳng đi qua \(S\) và song song với \(AB\).
B. Đường thẳng đi qua \(M\) và song song với \(SB\).
C. Đường thẳng đi qua \(M\) và song song với \(SC\).
D. Đường thẳng đi qua \(Q\) và song song với \(AB\).
-
Câu 36:
Cho các mệnh đề sau:
(1) Hai đường thẳng phân biệt không song song thì chéo nhau.
(2) Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng song song với hai đường thẳng đã cho.
(3) Nếu đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\) thì mọi đường thẳng nằm trong mặt phẳng\(\left( P \right)\) đều song song với \(a\).
Số mệnh đề đúng là?
A. 0
B. 1
C. 2
D. 3
-
Câu 37:
Cho hai đường thẳng chéo nhau \(a\) và \(b\). Lấy các điểm phân biệt \(A,\,B\in a;\,C,D\in b\). Khẳng định nào sau đây đúng?
A. \(AD\) cắt \(BC\).
B. \(AD\) và \(BC\) chéo nhau.
C. \(AD\) và \(BC\) đồng phẳng
D. \(AD\) song song với \(BC\).
-
Câu 38:
Cho hình chóp tứ giác \(S.ABCD\), \(AC\) và \(BD\) cắt nhau tại \(O\). Giao tuyến của hai mặt phẳng \(\left( SAC \right)\) và \(\left( SBD \right)\) là đường thẳng?
A. qua \(S\) và song song với \(AB\).
B. \(AC\).
C. qua \(S\) và song song với \(AB\).
D. \(SO\).
-
Câu 39:
Cho hai đường thẳng chéo nhau \(a\) và \(b\). Lấy hai điểm \(A,B\) phân biệt thuộc \(a\) và hai điểm \(C,D\) phân biệt thuộc \(b\). Khi đó hai đường thẳng \(A\text{D}\) và \(BC\) ở vị trí nào?
A. Chéo nhau.
B. song song nhau.
C. song song hoặc cắt nhau.
D. cắt nhau.
-
Câu 40:
Tìm mệnh đề đúng trong các mệnh đề dưới đây?
A. Hai đường thẳng không có điểm chung thì chéo nhau.
B. Hai đường thẳng chéo nhau thì không có điểm chung.
C. Hai đường thẳng nằm trên hai mặt phẳng phân biệt thì chéo nhau.
D. Hai đường thẳng không song song với nhau thì chéo nhau.