Đề thi giữa HK2 môn Toán 11 CD năm 2023-2024
Trường THPT Phạm Hồng Thái
-
Câu 1:
Khẳng định nào sau đây là đúng?
A. \({4^{ - 6}} = {6^{ - 4}}\)
B. \({4^{ - 6}} = \frac{1}{{{4^6}}}\)
C. \({4^{ - 6}} = \frac{1}{{{6^4}}}\)
D. \({4^{ - 6}} = {\left( { - 4} \right)^6}\)
-
Câu 2:
Chọn đáp án đúng. Cho số thực a và số nguyên dương n \(\left( {n \ge 2} \right)\). Số b được gọi là căn bậc n của số a nếu?
A. \({a^n} = b\)
B. \({b^n} = a\)
C. \(a.n = b\)
D. \(a.b = n\)
-
Câu 3:
Chọn đáp án đúng?
A. \(\sqrt[3]{{{{\left( {1 - \sqrt 5 } \right)}^3}}} = 1 - \sqrt 5 \)
B. \(\sqrt[3]{{{{\left( {1 - \sqrt 5 } \right)}^3}}} = - 1 - \sqrt 5 \)
C. \(\sqrt[3]{{{{\left( {1 - \sqrt 5 } \right)}^3}}} = - 1 + \sqrt 5 \)
D. \(\sqrt[3]{{{{\left( {1 - \sqrt 5 } \right)}^3}}} = 1 + \sqrt 5 \)
-
Câu 4:
Rút gọn biểu thức \(\left( {{9^{3 + \sqrt 3 }} - {9^{\sqrt 3 - 1}}} \right){.3^{ - 2\sqrt 3 }}\) được kết quả là?
A. \(\frac{{6560}}{9}\)
B. \(\frac{{6562}}{9}\)
C. \(\frac{{6560}}{3}\)
D. \(\frac{{6562}}{3}\)
-
Câu 5:
Cho a, b là các số thực dương. Rút gọn biểu thức \(\frac{{{{\left( {\sqrt[4]{{{a^3}{b^2}}}} \right)}^8}}}{{\sqrt[3]{{\sqrt {{a^{12}}{b^6}} }}}}\)?
A. \({a^2}{b^2}\)
B. \(ab\)
C. \({a^3}{b^4}\)
D. \({a^4}{b^3}\)
-
Câu 6:
Chọn đáp án đúng?
A. \(\ln {e^2} = {e^2}\)
B. \(\ln {e^2} = 2\)
C. \(\ln {e^2} = e\)
D. \(\ln {e^2} = \frac{1}{{{e^2}}}\)
-
Câu 7:
Chọn đáp án đúng. Cho a, b là các số thực dương. Giá trị của \(\ln \frac{a}{b} + \ln \frac{b}{a}\) bằng?
A. \(\ln \left( {ab} \right)\)
B. \(\ln \left( {\frac{a}{b} + \frac{b}{a}} \right)\)
C. 1
D. 0
-
Câu 8:
Chọn đáp án đúng. Cho \(a > 0,a \ne 1,b > 0\). Với mọi số nguyên dương \(n \ge 2\) ta có?
A. \({\log _a}\sqrt[n]{b} = n{\log _a}b\)
B. \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _a}b\)
C. \({\log _a}\sqrt[n]{b} = \frac{1}{n}{\log _b}a\)
D. \({\log _a}\sqrt[n]{b} = n{\log _b}a\)
-
Câu 9:
Cho \({\log _a}b = 4\). Giá trị của \({\log _a}\left( {{a^3}{b^2}} \right)\) bằng?
A. 12
B. 13
C. 14
D. 11
-
Câu 10:
Cho hai số thực dương a, b thỏa mãn \({a^3}{b^2} = 1000\). Giá trị của biểu thức \(P = 3\log a + 2\log b\) là?
A. 1
B. 2
C. 3
D. 4
-
Câu 11:
Trong các hàm số dưới đây, hàm số nào nghịch biến trên \(\left( {0; + \infty } \right)\)?
A. \(y = \ln 2x\)
B. \(y = {\log _{\frac{1}{\pi }}}x\)
C. \(y = {\log _{1 + \sqrt 3 }}x\)
D. \(y = \log x\)
-
Câu 12:
Hàm số nào dưới đây là hàm số đồng biến trên \(\mathbb{R}\)?
A. \(y = {3^x}\)
B. \(y = {\left( {\frac{1}{2}} \right)^x}\)
C. Cả A và B đều đúng
D. Cả A và b đều sai
-
Câu 13:
Đồ thị hàm số \(y = {6^{2x}}\) luôn đi qua điểm nào dưới đây?
A. (0; 1)
B. (0; -1)
C. (0; 6)
D. \(\left( {0;\frac{1}{6}} \right)\)
-
Câu 14:
Chọn đáp án đúng. Hàm số \(y = \log x\) có cơ số là?
A. 1
B. 10
C. e
D. Cả A, B, C đều sai
-
Câu 15:
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \(y = {\log _a}x,y = {\log _b}x,y = {\log _c}x\) thể hiện ở hình vẽ:
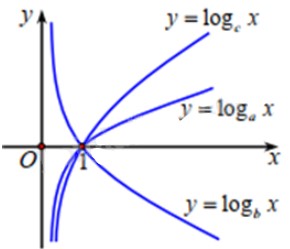
Khẳng định nào dưới đây là đúng?
A. \(b < c < a\)
B. \(b < a < c\)
C. \(a < b < c\)
D. \(a < c < b\)
-
Câu 16:
Tập xác định của hàm số \(y = \frac{1}{{\sqrt {3 - x} }} + \ln \left( {x - 1} \right)\) là?
A. \(D = \left[ {1;3} \right]\)
B. \(D = \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
C. \(D = \left( {1;3} \right)\)
D. \(D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
-
Câu 17:
Thống kê chiều cao của 40 học sinh lớp 11A (đơn vị: cm), ta có bảng số liệu sau:

Giá trị đại diện của nhóm \(\left[ {160;165} \right)\) là?
A. \(160cm\)
B. \(162,5cm\)
C. \(165cm\)
D. 16
-
Câu 18:
Nếu hai biến cố A và B độc lập và \(P\left( A \right) = 0,7,P\left( {AB} \right) = 0,28\) thì?
A. \(P\left( B \right) = 0,42\)
B. \(P\left( B \right) = 0,4\)
C. \(P\left( B \right) = 0,98\)
D. \(P\left( B \right) = 0,196\)
-
Câu 19:
Bảng tần số ghép nhóm cho ở bảng dưới:

Giá trị trung bình \(\overline x \) của nhóm mẫu số liệu là?
A. \(\overline x = \frac{{2\left( {{n_1}{x_1} + {n_2}{x_2} + ... + {n_m}{x_m}} \right)}}{n}\)
B. \(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_m}{x_m}}}{{2n}}\)
C. \(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_m}{x_m}}}{{n + 1}}\)
D. \(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_m}{x_m}}}{n}\)
-
Câu 20:
Chọn đáp án đúng.
Trong hộp kín có 6 quả bóng màu xanh và 8 quả bóng màu đỏ, các quả bóng có kích thước và khối lượng giống nhau. Lấy ngẫu nhiên đồng thời 2 quả bóng. Xét các biến cố:
A: “Hai quả bóng lấy ra có màu xanh”;
B: “Hai quả bóng lấy ra có màu đỏ”.
Biến cố hợp của hai biến cố A và B là?
A. Hai quả bóng lấy ra cùng có màu đỏ hoặc màu xanh
B. Hai quả bóng lấy ra có màu khác nhau
C. Hai quả bóng lấy ra không có quả nào màu đỏ
D. Hai quả bóng lấy ra không có quả nào màu xanh
-
Câu 21:
Một đội văn nghệ có 4 học sinh nam và 5 học sinh nữ. Giao viên phụ trách muốn chọn ra một đội tốp ca gồm 3 học sinh sao cho có cả nam và nữ cùng tham gia. Giáo viên có bao nhiêu cách chọn đội tốp ca như vậy?
A. 70 cách
B. 40 cách
C. 30 cách
D. 50 cách
-
Câu 22:
Cho A và B là hai biến cố độc lập với nhau. Biết rằng \(P\left( A \right) = 0,8\) và \(P\left( {AB} \right) = 0,4\). Xác suất của biến cố \(\overline A \overline B \) là?
A. 0,5
B. 0,2
C. 0,1
D. 0,3
-
Câu 23:
Bảng tần số ghép nhóm số liệu dưới đây thống kê kết quả kiểm môn toán của lớp 11E như sau:
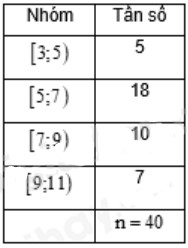
Mốt của mẫu số liệu ghép nhóm trên là (làm tròn kết quả đến hàng phần mười)?
A. 7,2
B. 7,5
C. 6,2
D. 6,5
-
Câu 24:
Cho hình hộp ABCD.A’B’C’D’ có các mặt là các hình vuông. Góc giữa hai đường thẳng AA’ và CD bằng:
A. \({90^0}\)
B. \({60^0}\)
C. \({30^0}\)
D. \({70^0}\)
-
Câu 25:
Cho tứ diện ABCD. Lấy điểm I bất kì thuộc cạnh AC. Qua I kẻ đường thẳng song song với AB cắt BC tại M. Qua I kẻ đường thẳng song song với CD cắt AD tại N. Khi đó, góc giữa hai đường thẳng AB và CD là?
A. \(\left( {IM,MN} \right)\)
B. \(\left( {IN,NM} \right)\)
C. \(\left( {IM,IN} \right)\)
D. \(\left( {IM,IC} \right)\)
-
Câu 26:
Cho hình chóp S. ABCD có ABCD là hình vuông cạnh bằng a và các cạnh bên đều bằng a. Gọi M, N lần lượt là trung điểm của AD, SD. Góc giữa hai đường thẳng MN và SC bằng?
A. \({60^0}\)
B. \({90^0}\)
C. \({30^0}\)
D. \({70^0}\)
-
Câu 27:
Cho hình chóp S. ABCD với đáy ABCD có tất cả các cạnh bằng nhau. Gọi I, J lần lượt thuộc các cạnh SC, BC sao cho tam giác IJC là tam giác đều. Khi đó, góc giữa hai đường thẳng IJ và AD bằng?
A. \({90^0}\)
B. \({120^0}\)
C. \({60^0}\)
D. \({70^0}\)
-
Câu 28:
Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\). Khẳng định nào sau đây là đúng?
A. \(SA \bot BC\)
B. \(SA \bot AC\)
C. \(SA \bot AB\)
D. Cả A, B, C đều đúng
-
Câu 29:
Cho hình hộp ABCD.A’B’C’D’ có \(AA' \bot \left( {ABCD} \right)\). Khẳng định nào dưới đây đúng?
A. (ABCD)\( \bot \) (A’B’C’D)
B. \(BB' \bot \left( {ABCD} \right)\)
C. Cả A và B đều đúng
D. Cả A và B đều sai
-
Câu 30:
Trong không gian, cho điểm A và mặt phẳng (P). Mệnh nào dưới đây đúng?
A. Có đúng hai đường thẳng đi qua A và vuông góc với (P)
B. Có đúng một đường thẳng đi qua A và vuông góc với (P)
C. Không tồn tại đường thẳng đi qua A và vuông góc với (P)
D. Có vô số đường thẳng đi qua A và vuông góc với (P)
-
Câu 31:
Phát biểu nào sau đây là đúng?
A. Nếu đường thẳng d vuông góc hai đường thẳng trong mặt phẳng (P) thì d vuông góc với tất cả các đường thẳng thuộc mặt phẳng (P).
B. Nếu đường thẳng d vuông góc với một đường thẳng trong mặt phẳng (P) thì d vuông góc với (P).
C. Nếu đường thẳng d vuông góc với hai đường thẳng bất kì trong mặt phẳng (P) thì d vuông góc với (P).
D. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau trong mặt phẳng (P) thì d vuông góc với (P).
-
Câu 32:
Cho tứ diện ABCD có ABC và BCD là các tam giác cân tại A và D. Gọi I là trung điểm của BC. Kẻ \(AH \bot DI\left( {H \in DI} \right)\). Hình chiếu vuông góc của A trên mặt phẳng (BCD) là?
A. I
B. H
C. D
D. C
-
Câu 33:
Cho hình chóp S. ABC có \(SA \bot \left( {ABC} \right)\), M là trung điểm của BC. Tam giác ABC cân tại A. Mệnh đề nào sau đây sai?
A. \(BC \bot SB\)
B. \(BC \bot SM\)
C. \(SA \bot BC\)
D. \(BC \bot AM\)
-
Câu 34:
Cho hình chóp S. ABCD có đáy ABCD là hình thoi và \(SA = SC,{\rm{ }}SB = SD\). Gọi O là giao điểm của AC và BD. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là?
A. A
B. C
C. O
D. D
-
Câu 35:
Cho tứ diện ABCD có \(DA \bot \left( {ABC} \right)\), ABC là tam giác cân tại A. Gọi M là trung điểm của BC. Gọi G, K lần lượt là trọng tâm của tam giác ABC và DBC. Góc giữa hai đường thẳng GK và AB bằng?
A. \({45^0}\)
B. \({60^0}\)
C. \({90^0}\)
D. \({70^0}\)
-
Câu 36:
Chọn đáp án đúng: Với n số thực dương \({b_1},{b_2},..,{b_n},a > 0,a \ne 1\) thì?
A. \({\log _a}\left( {{b_1}.{b_2}...{b_n}} \right) = {\log _a}{b_1} + {\log _a}{b_2} + ... + {\log _a}{b_n}\)
B. \({\log _a}\left( {{b_1}.{b_2}...{b_n}} \right) = {\log _a}{b_1}.{\log _a}{b_2}...{\log _a}{b_n}\)
C. \({\log _a}\left( {{b_1} + {b_2} + ... + {b_n}} \right) = {\log _a}{b_1}.{\log _a}{b_2}...{\log _a}{b_n}\)
D. \({\log _a}\left( {{b_1} + {b_2} + ... + {b_n}} \right) = {\log _a}{b_1} + {\log _a}{b_2} + ... + {\log _a}{b_n}\)
-
Câu 37:
Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\) với giá trị nào của a dưới đây?
A. \(a = \frac{1}{2}\)
B. \(a = 0,75\)
C. \(a = \frac{3}{2}\)
D. \(a = \ln 2\)
-
Câu 38:
Cho đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đồ thị là hình dưới đây: Tìm a?
A. \(a = 2\)
B. \(a = \sqrt 2 \)
C. \(a = \frac{1}{{\sqrt 2 }}\)
D. \(a = \frac{1}{2}\)
-
Câu 39:
Có bao nhiêu giá trị nguyên của a để hàm số \(y = {\left( { - {a^2} + 2a + 4} \right)^x}\) đồng biến trên \(\mathbb{R}\)?
A. 1
B. 2
C. 3
D. 4
-
Câu 40:
Một nhóm gồm 8 học sinh nam và 12 học sinh nữ. Chọn ra ngẫu nhiên 5 học sinh từ nhóm. Xác suất của biến cố: “Có ít nhất 3 học sinh nữ trong 5 học sinh vừa chọn” là?
A. \(\frac{{682}}{{969}}\)
B. \(\frac{{287}}{{969}}\)
C. \(\frac{{40}}{{57}}\)
D. \(\frac{{17}}{{57}}\)

.PNG)











