Đề thi giữa HK1 môn Toán 10 CTST năm 2023-2024
Trường THPT Lê Quý Đôn
-
Câu 1:
Trong các câu sau, câu nào là mệnh đề?
A. “Hà Nội”;
B. “Hà Nội là thủ đô của Việt Nam”;
C. “Hà Nội có phải thủ đô của Việt Nam không?”;
D. “Thủ đô của Việt Nam”.
-
Câu 2:
Đâu là mệnh đề chứa biến trong các câu dưới đây?
A. 2x là số chẵn;
B. 2 + 3 = 5;
C. 3 – 1 > 3;
D. 1 + 1 = 0.
-
Câu 3:
Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều sai thì ta suy ra điều gì?
A. P ⇔ Q;
B. P và Q là hai mệnh đề đảo;
C. P là mệnh đề phủ định của Q;
D. Không suy ra được gì.
-
Câu 4:
Chọn khẳng định đúng trong các khẳng định sau?
A. Mỗi tập hợp phải chứa ít nhất một phần tử;
B. Phần tử a không thuộc tập A kí hiệu là a ∈ A;
C. Tập hợp rỗng là con của mọi tập hợp;
D. Tập hợp không thể có vô số phần tử.
-
Câu 5:
Trong các tập hợp sau, tập hợp nào bằng nhau?
A. A = {0; 2; 4; 6; 8}, B = {x| x ∈ ℕ, x chia hết cho 2 và x < 12};
B. A = {2; 4; 6; 8}, B = {x| x ∈ ℕ, x chia hết cho 2 và x < 10};
C. A = {x| x ∈ ℕ, x chia hết cho 3 và x < 12}, B = {x| x ∈ ℕ, x chia hết cho 4 và x < 12};
D. A = {x| x ∈ ℕ, x ⋮ 2 và 2< x < 6}, B = {x| x ∈ ℕ, x chia hết cho 4 và 1 < x < 5}.
-
Câu 6:
Xác định M = A ∩ B trong trường hợp A là tập hợp các tam giác đều, B là tập hợp các tam giác cân?
A. M là tập hợp các tam giác cân;
B. M là tập hợp các tam giác đều;
C. M là tập hợp các đa giác;
D. M là tập hợp các tam giác.
-
Câu 7:
Xác định M = A ∪ B trong trường hợp A = {x | x ∈ ℕ, x ⋮ 4 và x < 10}, B là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 12?
A. M = {0; 3; 4; 6; 8; 9};
B. M = {0; 4; 6; 8; 9};
C. M = {0; 3; 4; 6; 8; 9; 12};
D. M = {0; 3; 6; 8; 9}.
-
Câu 8:
Lớp 10E của trường có 30 học sinh thích môn Vật lí, 15 học sinh thích môn Hóa học và 10 học sinh thích cả môn Vật lí và Hóa học. Hỏi lớp 10A có bao nhiêu học sinh chỉ thích Vật lí hoặc chỉ thích Hóa học biết mỗi học sinh của lớp đều thích môn Vật lí hoặc Hoá học?
A. 10
B. 15
C. 25
D. 30
-
Câu 9:
Hình vẽ sau biểu diễn miền nghiệm (phần không bị gạch) của bất phương trình bậc nhất hai ẩn nào?
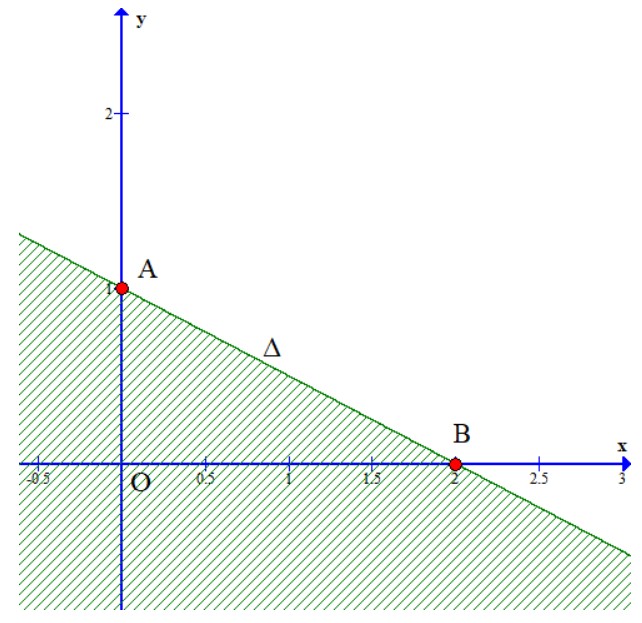
A. x + 2y – 2 > 0;
B. 3x + y – 2 < 0;
C. x – 2y + 1 < 0
D. x + 3y > 0.
-
Câu 10:
Chỉ ra câu sai trong các câu sau?
A. Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm;
B. Cặp số (2; 3) là nghiệm của bất phương trình 2x + 3y > 0;
C. Bất phương trình 2x + 5y < 1 có hệ số là a = 2; b = 5 và c = 1;
D. Bất phương trình bậc nhất hai ẩn có ít nhất một nghiệm.
-
Câu 11:
Khi x = 2 và y ≥ 0 thì bất phương trình sau có mấy cặp nghiệm nguyên: 2x + y < 6?
A. 0
B. 1
C. 2
D. 3
-
Câu 12:
Bác An cần phải làm nến trong vòng không quá 8 giờ để bán. Nến loại A cần 30 phút để làm xong một cây, nến loại B cần 1 giờ để làm xong một cây. Gọi x, y lần lượt là số nến loại A, B bác An sẽ làm được. Hệ bất phương trình mô tả điều kiện của x và y là hệ bất phương trình nào sau đây?
A. \(\left\{ \begin{matrix} x\ge 0 \\ y\ge 0 \\ 0,5x+y>8 \\ \end{matrix} \right.\)
B. \(\left\{ \begin{matrix} x\ge 0 \\ y\ge 0 \\ 0,5x+y\le 8 \\ \end{matrix} \right.\)
C. \(\left\{ \begin{matrix} x\ge 0 \\ y<0 \\ 0,5x+y\le 8 \\ \end{matrix} \right.\)
D. \(\left\{ \begin{matrix} x>0 \\ y>0 \\ 0,5x+y\le 8 \\ \end{matrix} \right.\)
-
Câu 13:
Cho hệ bất phương trình: \(\left\{ \begin{matrix} 2x+y>1 \\ x+y>3 \\ \end{matrix} \right.\), điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình đã cho?
A. O(0; 0);
B. M(2; 3);
C. N(3; 4);
D. P(4; 5).
-
Câu 14:
Khoảng giá trị của x khi y = 1 trong hệ bất phương trình \(\left\{ \begin{matrix} x+y\ge 1 \\ 2x-3y<5 \\ \end{matrix} \right.\) là?
A. x ∈ [0; 4);
B. x ∈ (0; 4];
C. x ∈ (1; 5);
D. x ∈ [1; 5].
-
Câu 15:
Cho α là góc tù. Khẳng định nào sau đây là đúng?
A. sin α < 0;
B. cos α > 0;
C. tan α < 0;
D. cot α > 0.
-
Câu 16:
Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 90°. Giá trị của biểu thức P = cosα.cosβ ‒ sinα.sinβ là?
A. P = 1;
B. P = 0;
C. P = ‒ 1;
D. P = 2.
-
Câu 17:
Giá trị của biểu thức: P = cos0° + cos1° + cos2° + ... + cos178° + cos179° + cos180° thuộc khoảng nào sau đây?
A. (0;1);
B. (1;2);
C. (‒1;1);
D. (‒1;0).
-
Câu 18:
Tam giác ABC có , AC = 10. Độ dài cạnh AB là?
A. 562;
B. 52;
C. 56;
D. 102.
-
Câu 19:
Tam giác ABC có \(AC=3\sqrt{3},~AB=3,~BC=6\). Số đo góc B là?
A. 30°;
B. 45°;
C. 60°;
D. 120°.
-
Câu 20:
Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù?
A. 105°;
B. 120°;
C. 135°;
D. 150°.
-
Câu 21:
Diện tích của tam giác ABC với AB = 20, AC = 10 là?
A. 50;
B. 502;
C. 503;
D. 50 5 ;
-
Câu 22:
Tam giác ABC có AB = 117. Độ dài cạnh AC là khoảng?
A. 118;
B. 68;
C. 168;
D. 200.
-
Câu 23:
Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Độ dài cạnh BC là khoảng?
A. 23;
B. 32;
C. 4;
D. 5.
-
Câu 24:
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.
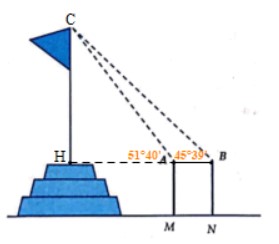
Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là?
A. 54,33 m;
B. 54,63 m;
C. 56,88 m;
D. 55,01 m.
-
Câu 25:
Cho hai vectơ không cùng phương và . Mệnh đề nào sau đây đúng?
A. Không có vectơ nào cùng phương với cả hai vectơ a→ và b→;
B. Có vô số vectơ cùng phương với cả hai vectơ a→ và b→;
C. Có một vectơ cùng phương với cả hai vectơ a→ và b→, đó là 0→;
D. Cả A, B, C đều sai.
-
Câu 26:
Cho hình vuông ABCD, khẳng định nào sau đây là đúng?
A. AB→=BC→;
B. AB→=CD→;
C. AC→=BD→;
D. AD→=CB→.
-
Câu 27:
Cho 5 điểm M, N, P, Q, R. Tính tổng ?
A. MR→;
B. MN→;
C. PR→;
D. MP→.
-
Câu 28:
Cho tam giác ABC đều có độ dài cạnh bằng a. Độ dài bằng?
A. a
B. 2a
C. a3;
D. a32.
-
Câu 29:
Cho hình bình hành ABCD. Hai điểm M, N lần lượt là trung điểm của BC và AD. Tìm đẳng thức sai?
A. AM→+AN→=AC→;
B. AM→+AN→=AB→+AD→;
C. AM→+AN→=MC→+NC→;
D. AM→+AN→=DB→.
-
Câu 30:
Cho hai lực và có cùng điểm đặt O và vuông góc với nhau. Cường độ của hai lực và lần lượt là 80N và 60N. Cường độ tổng hợp lực của hai lực đó là?
A. 100N;
B. 1003N;
C. 50N;
D. 503N.
-
Câu 31:
Cho ba điểm phân biệt A, B, C. Nếu \(\overrightarrow{AB}=-3\overrightarrow{AC}\) thì đẳng thức nào dưới đây đúng?
A. BC→=−4AC→;
B. BC→=−2AC→;
C. BC→=2AC→;
D. BC→=4AC→.
-
Câu 32:
Cho tam giác ABC. Gọi I là trung điểm AB. Tìm điểm M thỏa mãn hệ thức \(\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\vec{0}\)?
A. M là trung điểm BC;
B. M là trung điểm IC;
C. M là trung điểm IA;
D. M là điểm trên cạnh IC sao cho IM = 2MC.
-
Câu 33:
Cho hình bình hành ABCD, điểm M thỏa mãn \(4\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\). Xác định vị trí điểm M?
A. M là trung điểm AC;
B. Điểm M trùng với điểm C;
C. M là trung điểm AB;
D. M là trung điểm AD.
-
Câu 34:
Cho tam giác ABC và một điểm M tùy ý. Cho . Hãy xác định vị trí của điểm D sao cho ?
A. D là điểm thứ tư của hình bình hành ABCD;
B. D là điểm thứ tư của hình bình hành ACBD;
C. D là trọng tâm của tam giác ABC;
D. D là trực tâm của tam giác ABC.
-
Câu 35:
Tìm m để hàm số y = xác định trên khoảng (0; 5)?
A. 0 < m < 5;
B. m ≤ 0;
C. m ≥ 5;
D. m ≤ 0 hoặc m ≥ 5.
-
Câu 36:
Cho hàm số y = f(x) có đồ thị như hình vẽ:
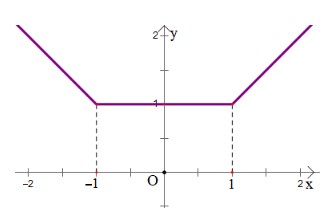
Khẳng định nào sau đây là đúng?
A. f(x) đồng biến trên khoảng (‒∞; ‒1);
B. f(x) nghịch biến trên khoảng (‒∞; 0);
C. f(x) đồng biến trên khoảng (1; +∞);
D. f(x) nghịch biến trên khoảng (‒1; 1).
-
Câu 37:
Hàm số y = 2x2 – 4x + 1 đồng biến và nghịch biến trên khoảng nào?
A. Hàm số nghịch biến trên khoảng (‒∞; 1] và đồng biến trên khoảng [1; +∞);
B. Hàm số nghịch biến trên khoảng (‒∞; 1) và đồng biến trên khoảng (1; +∞);
C. Hàm số đồng biến trên khoảng (‒∞; 1) và nghịch biến trên khoảng (1; +∞);
D. Hàm số đồng biến trên ℝ.
-
Câu 38:
Hàm số nào sau đây có đỉnh S(1; 0)?
A. y = 2x2 + 1;
B. y = x2 – 2x + 1;
C. y = x2;
D. y = 2x2 – 1.
-
Câu 39:
Cho hình chữ nhật ABCD có AB = , AD = 1. Tính góc giữa hai vectơ và ?
A. 89°;
B. 92°;
C. 109°;
D. 91°.
-
Câu 40:
Cho tam giác đều ABC có cạnh a. Tính tích vô hướng ?
A. AB→.AC→=2a2;
B. AB→.AC→=−a232;
C. AB→.AC→=−a22;
D. AB→.AC→=a22.











